Предмет: Алгебра,
автор: s21284697
СРОЧНО НАДО!!!!!!!
ДАЮ СТО БАЛОВ!!!!
Приложения:
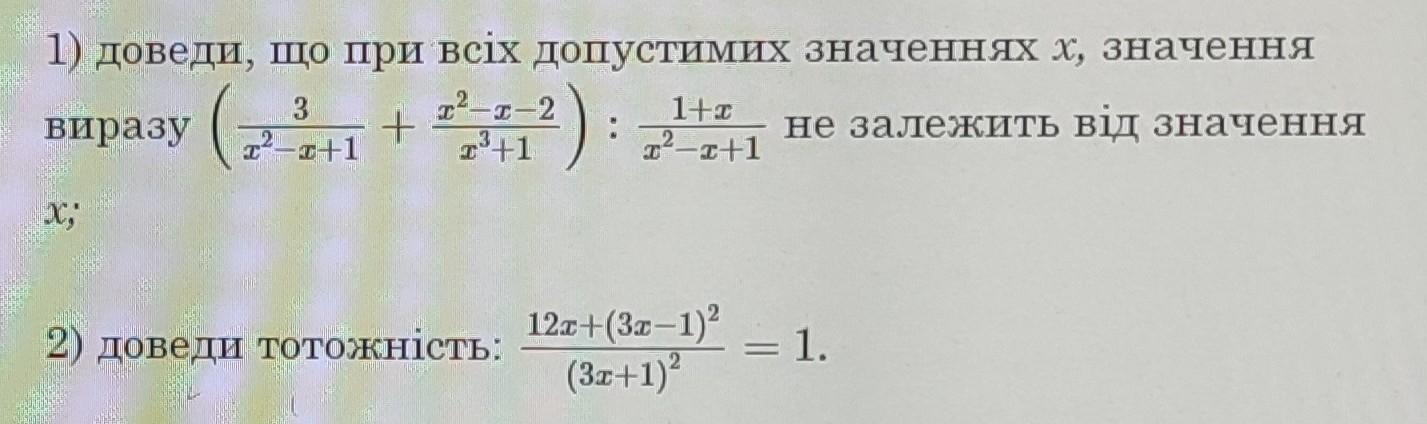
s21284697:
я написала
Ответы
Автор ответа:
1
Ответ:
1) Доказать, что выражение не зависит от переменной х . Применяем формулы сокращённого умножения .
Получили выражение , которое не зависит от переменной . Выражение равно константе .
2) Доказать тождество . Применяем формулы сокращённого умножения .
Тождество доказано .
Приложения:
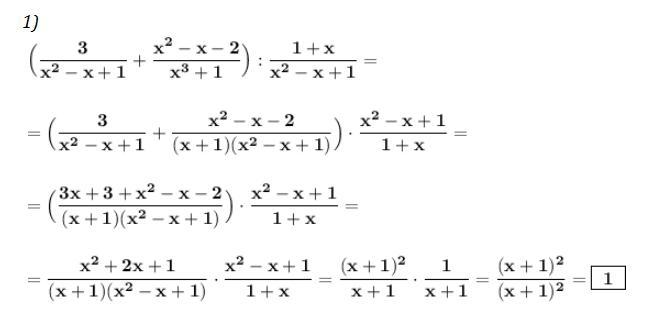
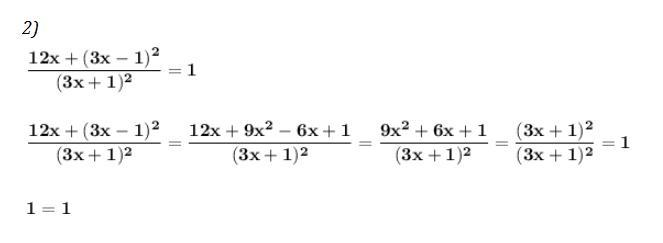

Похожие вопросы
Предмет: Алгебра,
автор: Warlord8567474
Предмет: Алгебра,
автор: silchuksasha16
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: ayaulym411
Предмет: Математика,
автор: Gswggdgs