Question

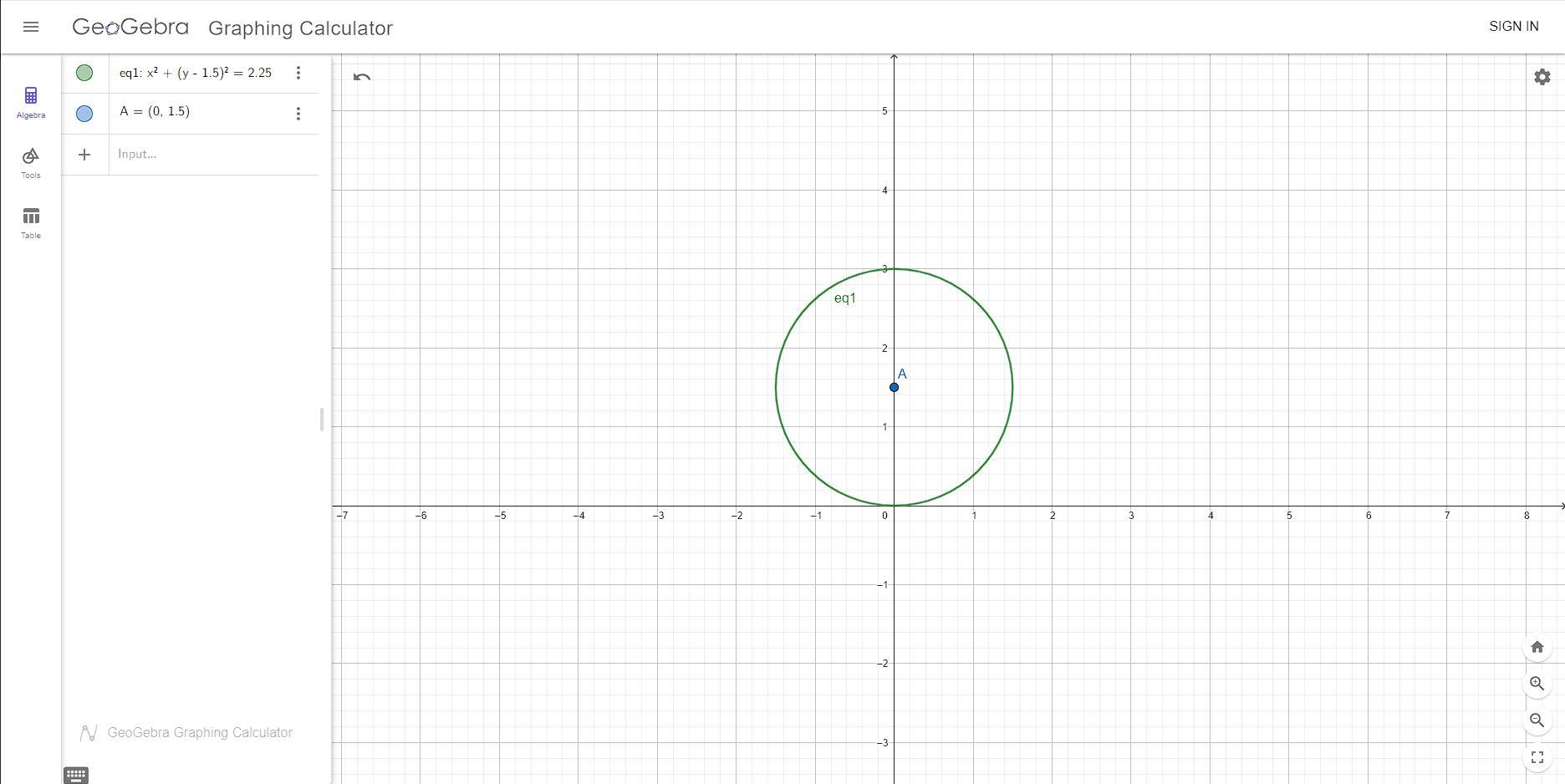
Определить полярные координаты центра и радиус окружности r=3sinα Построить ее. Записать уравнение в декартовых координа- тах.​

Answer 1

Ответ:

$r = \sqrt{x^2 + y^2}\\\sin \alpha = \cfrac{y}{r} = \cfrac{y}{\sqrt{x^2 + y^2}}\\r = 3 \sin \alpha\\\\\sqrt{x^2 + y^2} = \cfrac{3y}{\sqrt{x^2 + y^2}}\\x^2 + y^2 = 3y\\x^2 + y^2 - 3y = 0\\4x^2 + 4y^2 - 12y = 0\\4x^2 + 4y^2 - 2*2*3y + 9 = 9\\4x^2 + (2y - 3)^2 = 9\\4x^2 + 4(y - 1.5)^2 = 9\\x^2 + (y - 1.5)^2 = 2.25$

$x^2 + (y - 1.5)^2 = 2.25$ - уравнение в декартовых координатах

координаты центра окружности равны:

$(0, 1.5)$

Радиус окружности:

$\sqrt{2.25} = 1.5$