Скласти рiвняння кола, яке проходить через mочку D(- 8; - 2), якщо центр кола належить осі ордниот, а родіус дорівное 10. (x - a)2 + (y - b)2 = R2
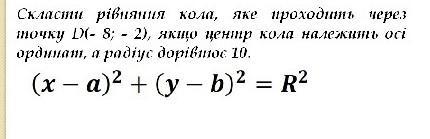
Ответы
Ответ:
x² + (y + 12)² = 100
Объяснение:
Рівняння кола виглядає так:
(x - a)² + (y - b)² = R²
У цьому рівнянні:
(a, b) - це координати центру кола.
R - радіус кола.
Знаючи, що центр кола належить осі ординат і маємо точку D(-8, -2) на колі з радіусом 10, можемо знайти центр кола (a, b) і підставити значення радіусу R:
Центр кола (a, b) лежить на осі ординат, тобто координата x центру a = 0 (оскільки вона співпадає з осьовою лінією). Знаючи, що радіус R = 10 і точка D(-8, -2) лежить на колі, можемо визначити координату y центру (b):
b = координата y точки D - радіус = -2 - 10 = -12.
Отже, координати центра кола (a, b) дорівнюють (0, -12), а радіус R = 10.
Підставляючи ці значення в загальне рівняння кола, отримаємо:
(x - 0)² + (y + 12)² = 10²
x² + (y + 12)² = 100