установіть графічно кількість коренів рівняння x⁵=3-2x
Ответы
Ответ:
Уравнение x⁵ = 3-2·x имеет один корень
Объяснение:
Требуется установить графически количество корней уравнения
x⁵ = 3-2·x.
Решение. Рассмотрим функции y = x⁵ и y = 3-2·x. Точка пересечения графиков этих функций как раз будут корнями уравнения x⁵ = 3-2·x.
Для построения графика необходимо выберем ряд точек, соответствующих значениям функции на заданных отрезках оси Оx.
Для функции y = x⁵ выберем значения для переменной x:
-2, -1, 0, 1, 2.
Теперь вычислим значения функции, соответствующие этим точкам:
y(-2) = (-2)⁵ = -32 ⇒ (-2; -32)
y(-1) = (-1)⁵ = -1 ⇒ (-1; -1)
y(0) = 0⁵ = 0 ⇒ (0; 0)
y(1) = 1⁵ = 1 ⇒ (1; 1)
y(2) = (2)⁵ = 32 ⇒ (2; 32).
График линейной функции y = 3–2·x - эта прямая. Для построения графика прямой достаточно 2 точки, через которых проходит эта прямая. Находим эти точки из уравнения функции:
1) x = 0 ⇒ y = 3–2·0 = 3 ⇒ (0; 3)
2) x = 1 ⇒ y = 3–2·1 = 1 ⇒ (1; 1).
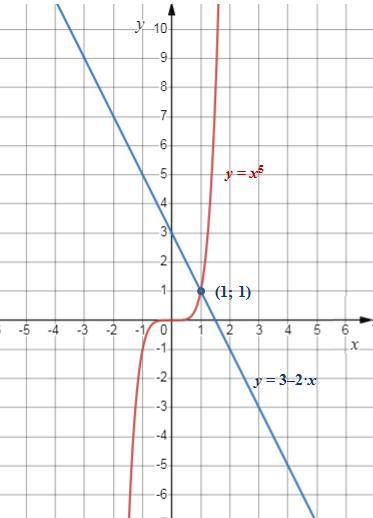
Отметим все точки в координатной плоскости и рисуем график функций y = x⁵ и y = 3-2·x (см. рисунок).
Из рисунка определяем, что функции y = x⁵ и y = 3-2·x пересекаются только в одной точке: (1; 1).
Значит, уравнение x⁵ = 3-2·x имеет один корень.
#SPJ1