Помогите с алгеброй пожалуйста!!!
а) 3x²+x+2>0
б) -3x²+2x-1≥0
в) 5x²-2x+1<0
г) -7x²+5x-2≤0
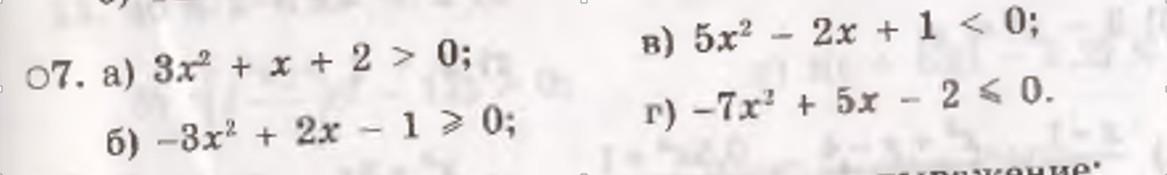
Ответы
Ответ:Займемося нерівностями:
а) 3x² + x + 2 > 0
Спростимо, використовуючи квадратичні нерівності:
3x² + x + 2 > 0
(3x + 2)(x + 1) > 0
Тепер знайдемо інтервали, на яких ця нерівність виконується:
Коли (3x + 2) > 0 та (x + 1) > 0: це відбувається, коли x > -2/3 та x > -1 (тобто x > -1).
Коли (3x + 2) < 0 та (x + 1) < 0: це відбувається, коли x < -2/3 та x < -1 (тобто x < -2/3).
Таким чином, рішення цієї нерівності - x < -2/3 або x > -1.
б) -3x² + 2x - 1 ≥ 0
Спростимо, використовуючи квадратичні нерівності:
-3x² + 2x - 1 ≥ 0
3x² - 2x + 1 ≤ 0
(3x - 1)² ≤ 0
Ця нерівність не має розв'язків, оскільки квадрат від'ємного числа не може бути дорівнювати нулю або бути меншим за нуль. Отже, рішення цієї нерівності - пуста множина.
в) 5x² - 2x + 1 < 0
Спростимо, використовуючи квадратичні нерівності:
5x² - 2x + 1 < 0
(5x - 1)² < 0
Як і в попередньому завданні, ця нерівність не має розв'язків, оскільки квадрат додатнього числа не може бути меншим за нуль. Рішення цієї нерівності - пуста множина.
г) -7x² + 5x - 2 ≤ 0
Спростимо, використовуючи квадратичні нерівності:
-7x² + 5x - 2 ≤ 0
(7x - 2)(x - 1) ≤ 0
Знайдемо інтервали, на яких ця нерівність виконується:
Коли (7x - 2) > 0 та (x - 1) > 0: це відбувається, коли x > 2/7 та x > 1 (тобто x > 1).
Коли (7x - 2) < 0 та (x - 1) < 0: це відбувається, коли x < 2/7 та x < 1 (тобто x < 2/7).
Таким чином, рішення цієї нерівності - 2/7 ≤ x ≤ 1.
Объяснение: