Предмет: Алгебра,
автор: tanyaxxs
розкрийте дужки, скоротіть дроби
Приложения:

Ответы
Автор ответа:
0
Ответ:
12.10. Раскрыть скобки . Применяем формулы сокращённого умножения .
12.11. Сократить дробь . Применяем формулы сокращённого умножения .
Приложения:

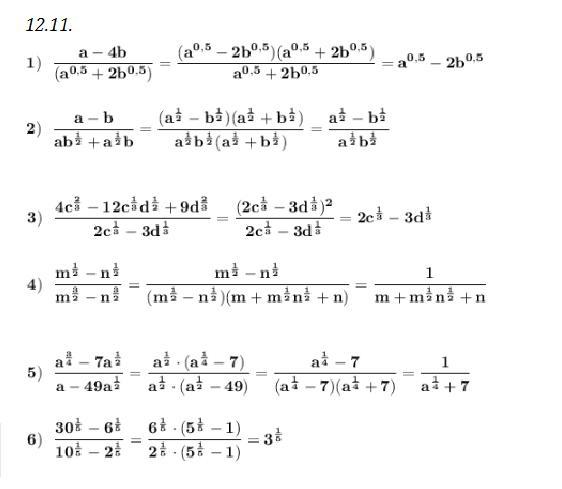

nurpromeermanov2006:
ЗДРАВСТВУЙТЕ ПОМГИТЕ ПОЖАЛУЙСТА С МАТЕМАТИКОЙ
у меня в профиле системы уравнений
не получается решить
Похожие вопросы
Предмет: Українська мова,
автор: maksimpugacis
Предмет: Физика,
автор: Ритка2008
Предмет: Литература,
автор: tiskovatatana19
Предмет: Другие предметы,
автор: albinabolatbek91
Предмет: Математика,
автор: alinamiruwu