3.3.° Знайдіть сторону AB трикутника ABC, якщо AC =√6 см, угол B = 120°, угол C = 45°.
Ответы
Привет держи, надеюсь помог :)
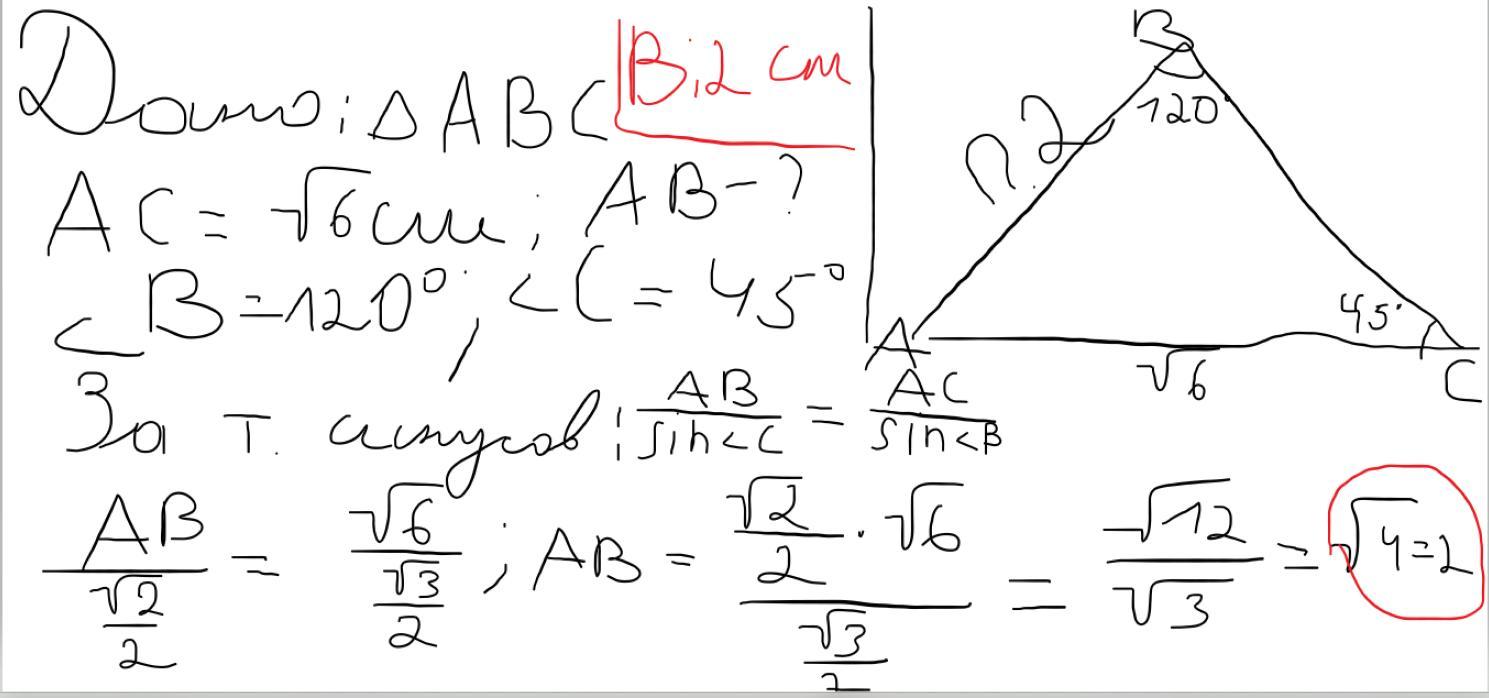
Ответ:
Для нахождения стороны AB в треугольнике ABC, можно использовать закон синусов, так как известны два угла и одна сторона.
Закон синусов утверждает:
\(\frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)}\)
где \(a\), \(b\), и \(c\) - стороны треугольника, \(A\), \(B\), и \(C\) - противолежащие им углы.
В данном случае, известно \(AC = \sqrt{6}\) см (сторона \(c\)), \(B = 120^\circ\) (угол \(B\)) и \(C = 45^\circ\) (угол \(C\)). Нам нужно найти сторону \(AB\) (пусть это будет \(a\)).
Применяя закон синусов:
\(\frac{a}{\sin(A)} = \frac{\sqrt{6}}{\sin(120^\circ)}\)
Угол \(A\) можно найти, используя сумму углов в треугольнике:
\(A = 180^\circ - B - C = 180^\circ - 120^\circ - 45^\circ = 15^\circ\)
Теперь мы можем использовать значение \(A\) и выразить \(a\):
\(\frac{a}{\sin(15^\circ)} = \frac{\sqrt{6}}{\sin(120^\circ)}\)
\(a = \frac{\sin(15^\circ) \cdot \sqrt{6}}{\sin(120^\circ)}\)
Теперь, вычислим \(a\):
\(a \approx 2.11\) см
Итак, сторона \(AB\) треугольника ABC примерно равна 2.11 см.