Предмет: Алгебра,
автор: kotpilot19
ПОМОГИТЕ ПОЖАЛУЙСТА, 3 ЗАДАНИЕ СРОЧНО
ДАЮ 50 БАЛЛОВ
Приложения:
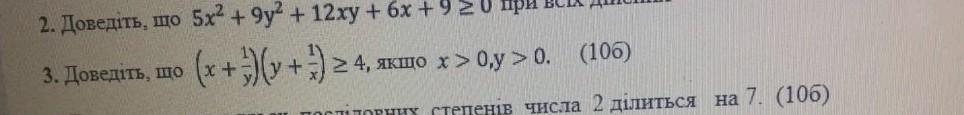
Ответы
Автор ответа:
0
Ответ:
Объяснение:
формула:
Похожие вопросы
Предмет: Литература,
автор: hzuzer521
Предмет: История,
автор: Krinitski
Предмет: Другие предметы,
автор: veta55995
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: wonkaocc