Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Розв'язати систему рівнянь.
Приложения:
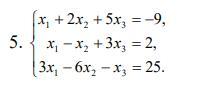
Ответы
Автор ответа:
2
Ответ:
2; -3; -1
Объяснение:
Решить систему методом Крамера.
Определитель основной матрицы:
Δ ≠ 0 ⇒ можем применить формулу Крамера.
Найдем определитель .
Заменим первый столбец на столбец свободных членов:
Найдем определитель .
Заменим второй столбец на столбец свободных членов:
Найдем определитель .
Заменим третий столбец на столбец свободных членов:
Теперь по формуле Крамера получим ответ:
Приложения:

di4824041:
здравствуйте, помогите пожалуйста с вопросом по геометрии
Две равные боковые грани пирамиды DABC перпендикулярны основанию, а третья грань образует с основанием двуранный угол ра...
https://znanija.com/task/53814793?utm_source=android&utm_medium=share&utm_campaign=question
https://znanija.com/task/53814793?utm_source=android&utm_medium=share&utm_campaign=question
спасибо большое)
natalyabryukhova, здравствуйте! можете помочь пожалуйста? https://znanija.com/task/53823450
Похожие вопросы
Предмет: География,
автор: pupsikkk20
Предмет: Английский язык,
автор: kazarukelizaveta
Предмет: Физика,
автор: najsmilli
Предмет: Алгебра,
автор: Ekaterina943
Предмет: Химия,
автор: Larisabusheva1506