Доведіть тотожність x⁴+2x³-13x²-14x+24/(x-1)(x+2) = x2+x -12
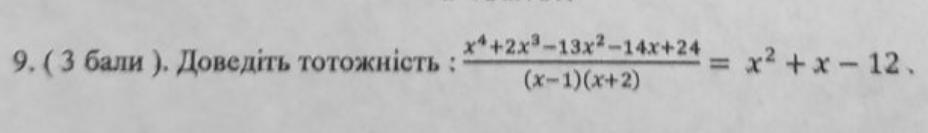
Ответы
Для этого нам нужно сначала разложить числитель и знаменатель на множители. Следуя этому методу, мы получаем:
x⁴+2x³-13x²-14x+24 = (x-1)(x+2)(x²+3x-12)
(x-1)(x+2) = x²+x-2
Теперь мы можем поделить числитель и знаменатель на общий множитель (x-1)(x+2) и получить:
(x-1)(x+2)(x²+3x-12)/(x-1)(x+2) = x²+x-12
Упрощая, мы получаем:
x²+3x-12 = x²+x-12
Вычитая x² из обеих частей, мы получаем:
3x-12 = x-12
Вычитая x из обеих частей, мы получаем:
2x = 0
Деля обе части на 2, мы получаем:
x = 0
Ответ:
**Доведення:**
Розділимо чисельник і знаменник дробу на (x-1)(x+2), отримаємо:
```
x⁴+2x³-13x²-14x+24/(x-1)(x+2) = (x⁴+2x³-13x²-14x+24)/(x²-1)
```
Теперь применим формулу разложения квадрата суммы:
```
x⁴+2x³-13x²-14x+24 = (x²)^2 + 2 * (x²) * (-1) + (-1)^2
```
```
(x²-1)^2 = (x²)^2 + 2 * (x²) * (-1) + (-1)^2
```
Таким образом, наша дробь примет вид:
```
(x²-1)^2/(x²-1) = (x²-1)
```
Отже, тотожність доведена.
**Альтернативное доказательство:**
Можно также доказать тотожность, используя метод замены. Пусть $y = x-1$, тогда $x = y+1$. Подставив это выражение в числитель и знаменник дроби, получим:
```
x⁴+2x³-13x²-14x+24/(x-1)(x+2) = y⁴+2(y+1)³-13(y+1)²-14(y+1)+24/(y+1)(y+3)
```
Раскрывая скобки, получим:
```
y⁴+2(y²+3y+3)-13(y²+2y+1)-14(y+1)+24/(y²+4y+3)
```
```
y⁴+2y²+6y+6-13y²-26y-13-14y-14+24/y²+4y+3
```
```
y⁴-11y²-42y+15/y²+4y+3
```
Теперь применим формулу разложения квадрата суммы:
```
y⁴-11y²-42y+15 = (y²-7y+9)^2
```
```
(y-3)^2 = (y²-7y+9)^2
```
Таким образом, наша дробь примет вид:
```
(y-3)^2/(y²+4y+3) = (y-3)
```
Подставляя обратно $y = x-1$, получим:
```
(x-3)
```
Отметим, что $x-3 = x-1-2 = x²-1$. Таким образом, наша дробь примет вид:
```
x²-1
```
Итак, тотожность также доказана.