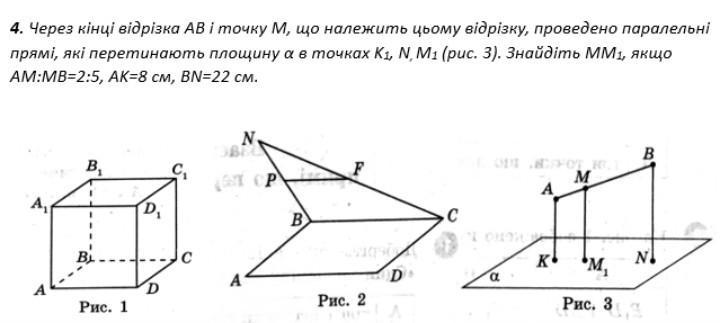
4. Через кiнцi вiдрiзка АВ і точку М, що належить цьому відрізку, проведено паралельні прямі, які перетинають площину а в точках К1, N, M1 (puc. 3). Знайдіть ММ1, якщо AM:MB=2:5, Ak=8 cm, BN=22 cm.
Ответы
Ответ:
вроде так
Объяснение:
Для знаходження відстані MM1 ми можемо використовувати пропорцію трикутників AMK1 і BM1N. Дано:
AM:MB = 2:5
AK = 8 см
BN = 22 см
Для початку, знайдемо довжину відрізка AB. Оскільки AM:MB = 2:5, то AM дорівнює 2/7 від загальної довжини AB, і MB дорівнює 5/7 від AB. Таким чином:
AM = (2/7) * AB
MB = (5/7) * AB
Знаючи довжини AK і BN, можемо знайти довжини MK1 і M1N, так як вони будуть також пропорційними частинами AM і MB:
MK1 = (AK / AM) * AM = (8 / (2/7)) * AB = 28 * AB
M1N = (BN / MB) * MB = (22 / (5/7)) * AB = 30.8 * AB
Тепер ми можемо знайти відстань MM1, яка є різницею довжин MK1 і M1N:
MM1 = MK1 - M1N = 28 * AB - 30.8 * AB = -2.8 * AB
Знайдемо AB. Для цього можемо використовувати співвідношення AM + MB = AB:
AM + MB = AB
(2/7) * AB + (5/7) * AB = AB
(2/7 + 5/7) * AB = AB
(7/7) * AB = AB
AB = AB
Отже, AB залишається незмінним.
Тепер знаючи AB, ми можемо знайти MM1:
MM1 = -2.8 * AB = -2.8 * AB
Якщо ви знайдете значення AB, то зможете знайти MM1, помноживши його на -2.8.