Предмет: Математика,
автор: CVING
50 Баллов. СРОЧНО!Вычислить при помощи определенного интеграла площадь фигуры, ограниченной графиком функции y=x²-3x и осью Ox с рисунком
Ответы
Автор ответа:
0
Ответ: 4.5 кв. ед.
Пошаговое объяснение:
Вычислить при помощи определенного интеграла площадь фигуры y=x²-3x и осью Ox.
************
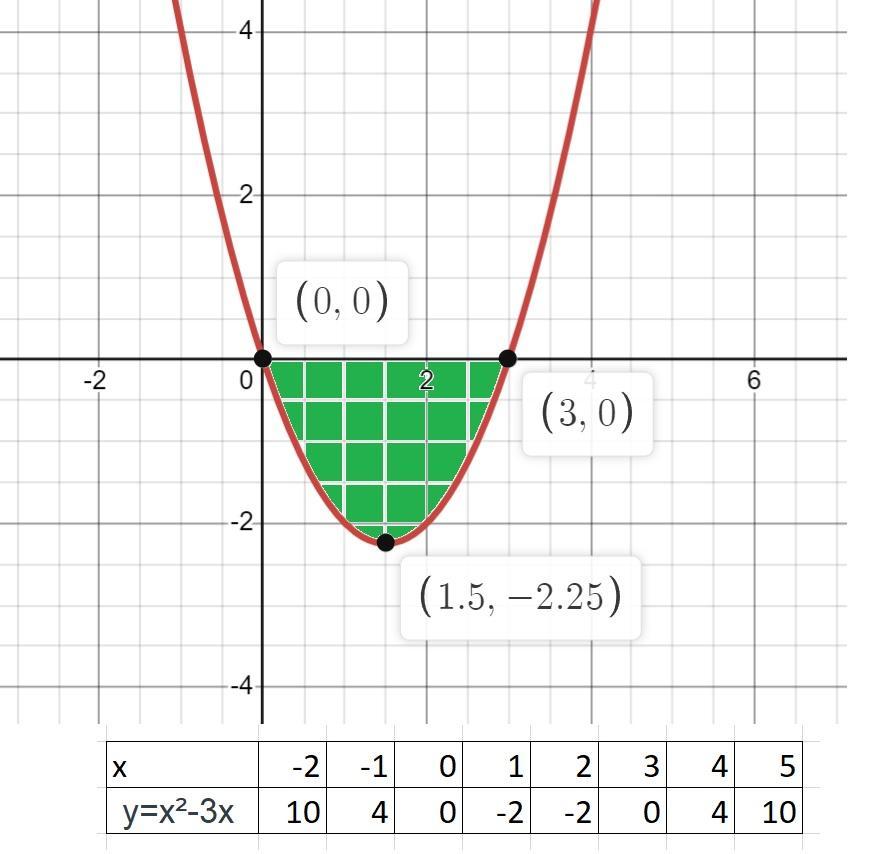
строим график функции y=x²-3x. (См. скриншот).
Площадь криволинейной трапеции определяется по формуле
S=∫(a;b)f₁(x) - ∫(a;b)f₂(x)dx, где:
Находим по графику пределы интегрирования: a=0; b=3.
Функции f₁(x) = 0; f₂(x) = x²-3x.
Тогда S = ∫(0;3)0dx - ∫(0;3) (x²-3x)dx =0-∫(0;3) x²dx + 3∫(0;3)xdx =
= -1/3(x³)|(0;3) +3/2(x²)|(0;3) =-1/3(3³-0³) + 3/2(3²-0²) = = -27/3 + 27/2 = 9/2 =
= 4.5 кв. ед.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: qulmatovagulnora38
Предмет: Физика,
автор: RandomPeopleIn
Предмет: Литература,
автор: maksimvoronkovmailru
Предмет: Математика,
автор: xtzqqq
Предмет: Математика,
автор: s57756339