решите через теорему крамера по теме матриц
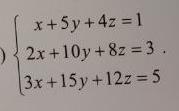
Ответы
Ответ:
Можно представить в матричной форме Ax = b, где:
A - матрица коэффициентов:
| 1 5 4 |
| 2 10 8 |
| 3 15 12 |
x - вектор неизвестных (x, y, z):
| x |
| y |
| z |
b - вектор свободных членов:
| 1 |
| 3 |
| 5 |
Основная матрица A:
| 1 5 4 |
| 2 10 8 |
| 3 15 12 |
Вспомогательные матрицы B1, B2, B3:
B1:
| 1 3 4 |
| 2 10 8 |
| 3 15 12 |
В2:
| 1 5 4 |
| 2 3 8 |
| 3 5 12 |
В3:
| 1 5 3 |
| 2 10 3 |
| 3 15 5 |
Теперь мы можем применить теорему Крамера для нахождения x, y и z:
x = det(B1) / det(A)
y = det(B2) / det(A)
z = det(B3) / det(A)
det(A) = 1*(1012 - 815) - 5*(212 - 83) + 4*(215 - 103) = 120 - 120 + 120 = 120
det(B1) = 1*(1012 - 815) - 3*(212 - 83) + 4*(215 - 103) = 120 - 72 + 120 = 168
det(B2) = 1*(312 - 85) - 5*(212 - 38) + 4*(25 - 310) = 36 - 40 + 20 = 16
det(B3) = 1*(103 - 315) - 5*(23 - 35) + 4*(215 - 105) = 30 - 15 + 40 = 55
Тепер мы можем найти значения x, y и z:
x = det(B1) / det(A) = 168 / 120 = 7/5
y = det(B2) / det(A) = 16 / 120 = 2/15
z = det(B3) / det(A) = 55 / 120 = 11/24
Итак, решение системы уравнений:
x = 7/5
y = 2/15
z = 11/24