Предмет: Геометрия,
автор: yapayaka
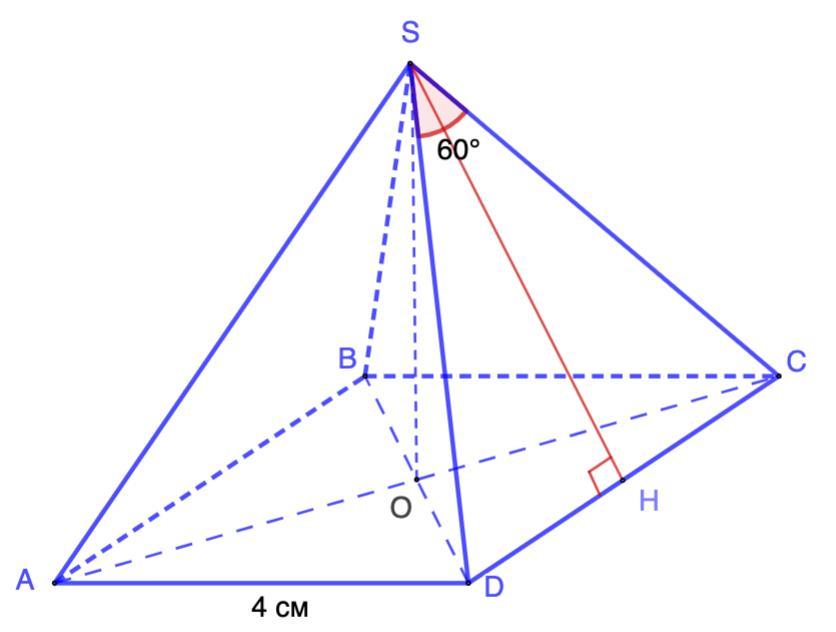
Сторона основи правильної чотирикутної піраміди дорівнює 4 см, а плоский кут при вершині дорівнює 60°. Обчисліть площу бічної поверхні.
Чекаю на розгорнуту відповідь (малюнок, повна умова та розписане розв'язання). Буду дуже вдячна за допомогу!
Ответы
Автор ответа:
1
Ответ:
Площадь боковой поверхности равна 16√3 см².
Объяснение:
Сторона основания правильной четырехугольной пирамиды равна 4 см, а плоский угол при вершине равен 60°. Вычислите площадь боковой поверхности.
Дано: SABCD - правильная пирамида;
АВ = ВС = CD = AD = 4 см; ∠DSC = 60°°.
Найти: S бок.
Решение:
- Основание правильной четырехугольной пирамиды - квадрат, боковые грани - равные равнобедренные треугольники.
- Площадь боковой поверхности правильной пирамиды равна:
,
где l - апофема.
- Апофема - высота боковой стороны.
Периметр основания равен:
P осн. = 4 · AB = 4 · 4 = 16 (см)
Найдем апофему.
Рассмотрим ΔDSC - равнобедренный.
- Если в равнобедренном треугольнике есть угол 60°, то он равносторонний.
⇒ ∠SDC = ∠SCD = 60°; DC = SD = SC = 4 см.
Рассмотрим ΔDSH - прямоугольный.
- Синус угла - отношение противолежащего катета к гипотенузе.
S бок. = 1/2 · 16 · 2√3 = 16√3 (см²)
Площадь боковой поверхности равна 16√3 см².
Приложения:
Похожие вопросы
Предмет: Биология,
автор: nasttka17
Предмет: Математика,
автор: salahovakemale44
Предмет: Алгебра,
автор: karmanrenata764
Предмет: Алгебра,
автор: vladykaelizaveta7
Предмет: Математика,
автор: boksunz