Предмет: Математика,
автор: 1Kolomiets1
Дослідити на збіжність ряд
Приложения:
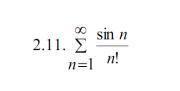
Ответы
Автор ответа:
0
Ответ:
Ряд сходится.
Пошаговое объяснение:
последовательность sin(n) ограничен слева и справа
-1 ≤ sin(n) ≤ sin(n)
Тогда мы можем сказать, что для ∀ n справедливо
По признаку Даламбера исследуем ряд
Ряд будет сходиться, если сходится ряд
.
если q < 1, то ряд сходится.
наше значение q (=0) < 1, значит, ряд сходится.
А тогда сходится и исходный ряд .
Похожие вопросы
Предмет: Математика,
автор: emin75626
Предмет: География,
автор: nqy2hrrwwj
Предмет: Биология,
автор: davidnesviteev
Предмет: Русский язык,
автор: Uhvygctfx40
Предмет: Физика,
автор: alinadmitrievna81