Предмет: Алгебра,
автор: taetaejkforver
Очень важно сделать на листке!
Приложения:

Ответы
Автор ответа:
0
Ответ:
Преобразуем выражение. Применим основное тригонометрическое тождество и формулу косинуса двойного угла :
Вычислим интеграл , применяя только что доказанное равенство . Получим табличные интегралы .
Приложения:
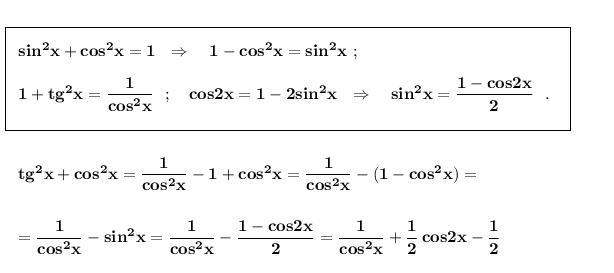
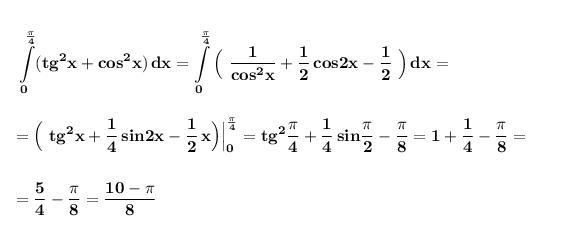
Похожие вопросы
Предмет: Литература,
автор: artur563
Предмет: История,
автор: aliue4734
Предмет: Математика,
автор: azikakhasanova2013
Предмет: Физика,
автор: blinovdima
Предмет: История,
автор: Dnelya