Предмет: Алгебра,
автор: masha01021
Помогите пожалуйста решить, подробнее пожалуйста
Приложения:
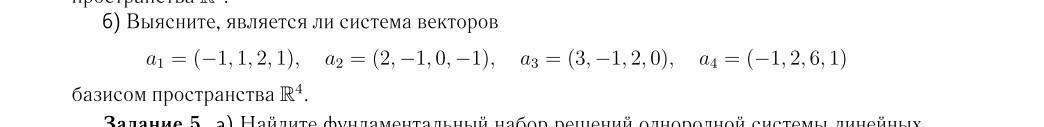
Ответы
Автор ответа:
2
Ответ:
данная система не вляется базисом.
Объяснение:
Векторное уравнение
В матричном виде
Решаем методом Гаусса.
первую строку *(-1)
2 строка - 1 строка;
от 3 строки отнять 1 строку, предварительно умноженную на 2;
4 строка - 1 строка.
к 1 строке добавить 2 строку, предварительно умноженную на 2;
от 3 строки отнять 2 строку, предварительно умноженную на 4;
от 4 строки отнять 2 строку, предварительно умноженную на 3.
поменять местами 3-ую и 4-ую строки
теперь 3-ую строку : (-3)
и, наконец,
от 1 строки отнять 3 строку, предварительно умноженную на 1;
от 2 строки отнимаем 3 строку, предварительно умноженную на 2.
И вот получим
Мы видим, что у нас есть , данная система векторов не является базисом.
masha01021:
спасибо большое,
Похожие вопросы
Предмет: Английский язык,
автор: dianaharcenko762
Предмет: Литература,
автор: angel254789324
Предмет: Литература,
автор: ekaterinanosenko11
Предмет: Физика,
автор: eremiansilva
Предмет: Математика,
автор: kristinagural532