Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Знайти границі послідовності. n -->∞
Приложения:
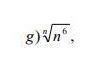
fctdgsygfdhngfxzgsac:
Найти пределы последовательности
Ответы
Автор ответа:
1
Ответ: .
Найти предел последовательности , общий член которой
Докажем сначала, что .
Найдём предварительно предел от логарифма :
По правилу Лопиталя имеем :
Знак предела и непрерывной функции можно менять местами , получим
По свойству логарифма , если .
Поэтому из того, что следует, что
.
Исходя из этого доказывается, что .
Найдём предел последовательности .
.
Приложения:

спасибо большое))
Похожие вопросы
Предмет: Физика,
автор: mihailaliminari
Предмет: Физика,
автор: flytpa12
Предмет: География,
автор: polinaskorod11w
Предмет: Русский язык,
автор: Аноним