Предмет: Математика,
автор: mutzakden
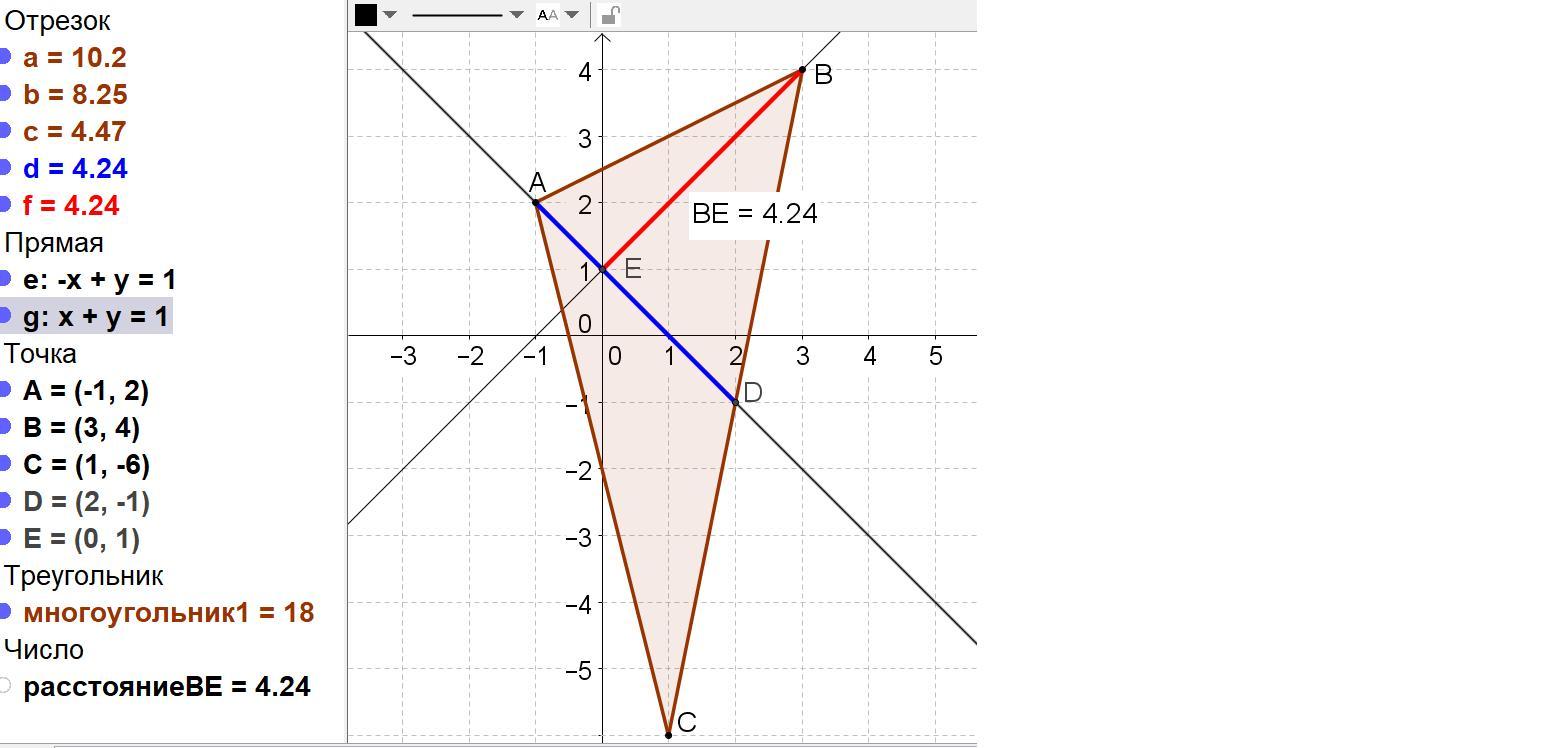
Дано трикутник з вершинами A(−1;2), B(3;4), C (1;−6). Обчислити відстань від вершини B до медіани, яка проведена із вершини A . Зробити рисунок.
Ответы
Автор ответа:
0
Находим координаты точки D как середины стороны ВС.
D = (B(3;4) + C(1;−6))/2 = (2; -1).
Уравнение медианы АD: (x + 1)/(2-(-1) = (y – 2)/(-1-2) = (x + 1)/3 = (y – 2)/(-3) каноническое, -3x – 3 = 3y – 6 или x + y -1 = 0 общее.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = (A·Mx + B·My + C)/√A2 + B2
Подставим в формулу данные: координаты точки B(3; 4) и уравнение прямой АD: x + y -1 = 0
d = (1·3 + 1·4 - 1)/√12 + 12 = (3 + 4 - 1)/√2 = 6/√2 ≈ 4,24264.
Ответ: d = 6/√2 ≈ 4,24264.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: polinagontar2
Предмет: Українська мова,
автор: vitalinatopchiy
Предмет: ОБЖ,
автор: Useruuususbjs
Предмет: Математика,
автор: sos4710
Предмет: Русский язык,
автор: nigayaleksandr514