Предмет: Алгебра,
автор: nastyaboiko29
ДОПОМОЖУ ДУЖЕ ПРОШУ ДАЮ 50 БАЛІВ
Приложения:
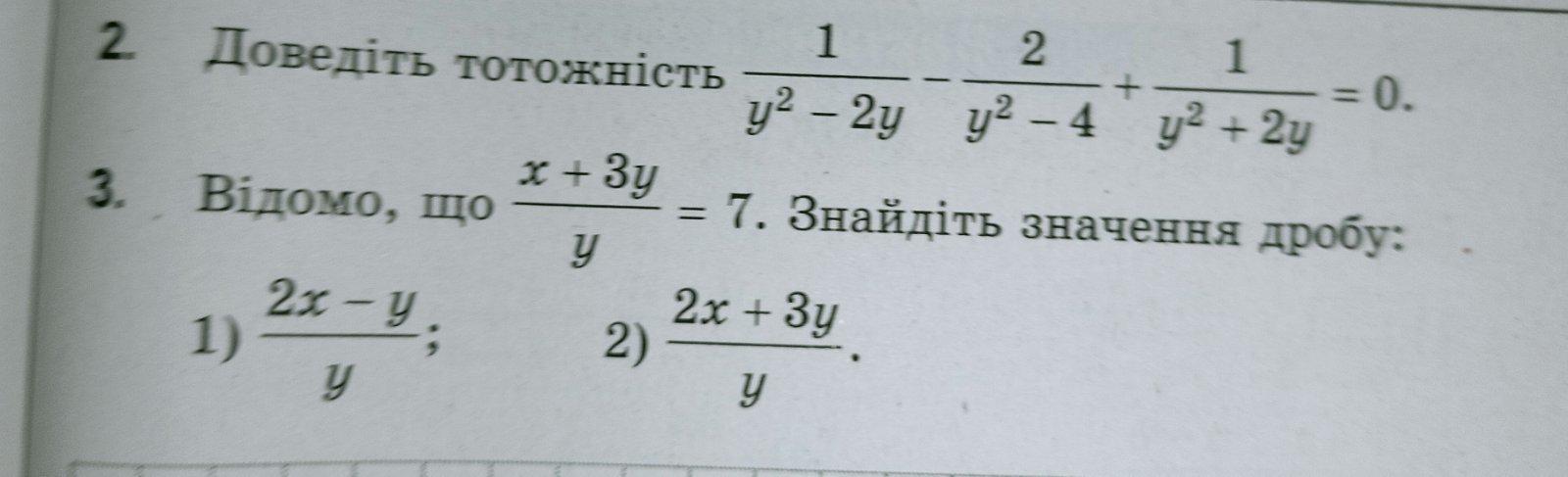
Ответы
Автор ответа:
1
Ответ:
2.а) 7
2.б) 11
Объяснение:
1)
Рассмотрим левую часть
Доказано
2) По условию:
a)
б)
nastyaboiko29:
ДЯКУЮЮЮЮЮЮ ВЕЛИКЕ
Похожие вопросы
Предмет: Немецкий язык,
автор: mmbtvaa
Предмет: Українська мова,
автор: TupaBog
Предмет: Геометрия,
автор: ddjddjdjejejejejejdd
Предмет: Қазақ тiлi,
автор: burkytbaevamaral
Предмет: Математика,
автор: kozbagarovaelmira