Предмет: Алгебра,
автор: yrcenko666
log в степени 2 0,5х-log0,5x-2≥0
Приложения:
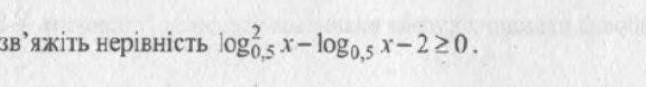
Ответы
Автор ответа:
4
Решить логарифмическое неравенство:
Решение:
Сделаем замену:
Получим квадратное неравенство:
Найдём корни квадратного уравнения по теореме Виета:
Решаем неравенство, используя метод интервалов:
+ - +
/////////// -1 .............2//////////
Получаем совокупность двух неравенств:
Обратная замена:
или
или
Так как основание логарифма 0.5 < 1 ,то функция убывает, знак неравенства меняется на противоположный.
Тогда получим
или
Учитывая ОДЗ х>0, запишем
Ответ:
x∈(0;0.25] ∪ [2;+∞)
Автор ответа:
3
Відповідь: фото.
Пояснення:
розв'язання завдання додаю
Приложения:

Похожие вопросы
Предмет: Химия,
автор: Mixajj
Предмет: Қазақ тiлi,
автор: aroslavvajs8
Предмет: Литература,
автор: noter3744
Предмет: Другие предметы,
автор: zakanerkenaz