Предмет: Алгебра,
автор: Xxxli09
Очень срочно я щас на уроке дам 55 балов
Приложения:
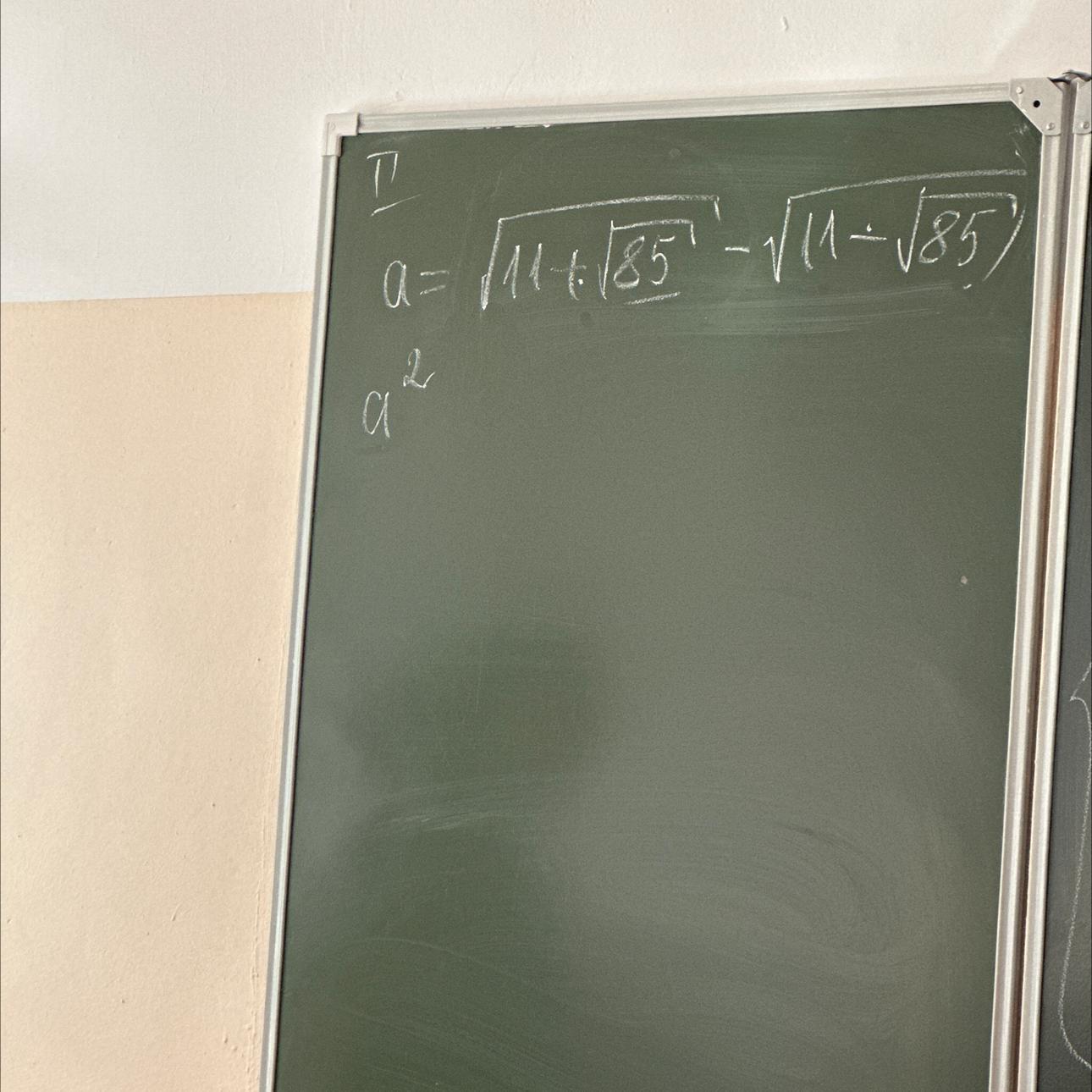
Ответы
Автор ответа:
2
Решение .
Представим подкоренные выражения в виде полных квадратов .
Теперь вычислим значение выражения .
Приложения:


Xxxli09:
Спасибо большое)
Пожалуйста
здравствуйте помогите пожалуйста решить задачу
Похожие вопросы
Предмет: Математика,
автор: vasilievandrij
Предмет: Математика,
автор: noynameeeeeeeeeee
Предмет: Українська мова,
автор: bobkovamilana457
Предмет: Алгебра,
автор: flexdope36