Предмет: Геометрия,
автор: sovochka0240
Два однакових рівносторонніх трикутника ABC i СДЕ мають спільну вершину С. Знайдіть ² АВД, якщо ²АСД = 80 °.
Ответы
Автор ответа:
7
Ответ:
∠АВД=40°
Объяснение:
Вірна умова:
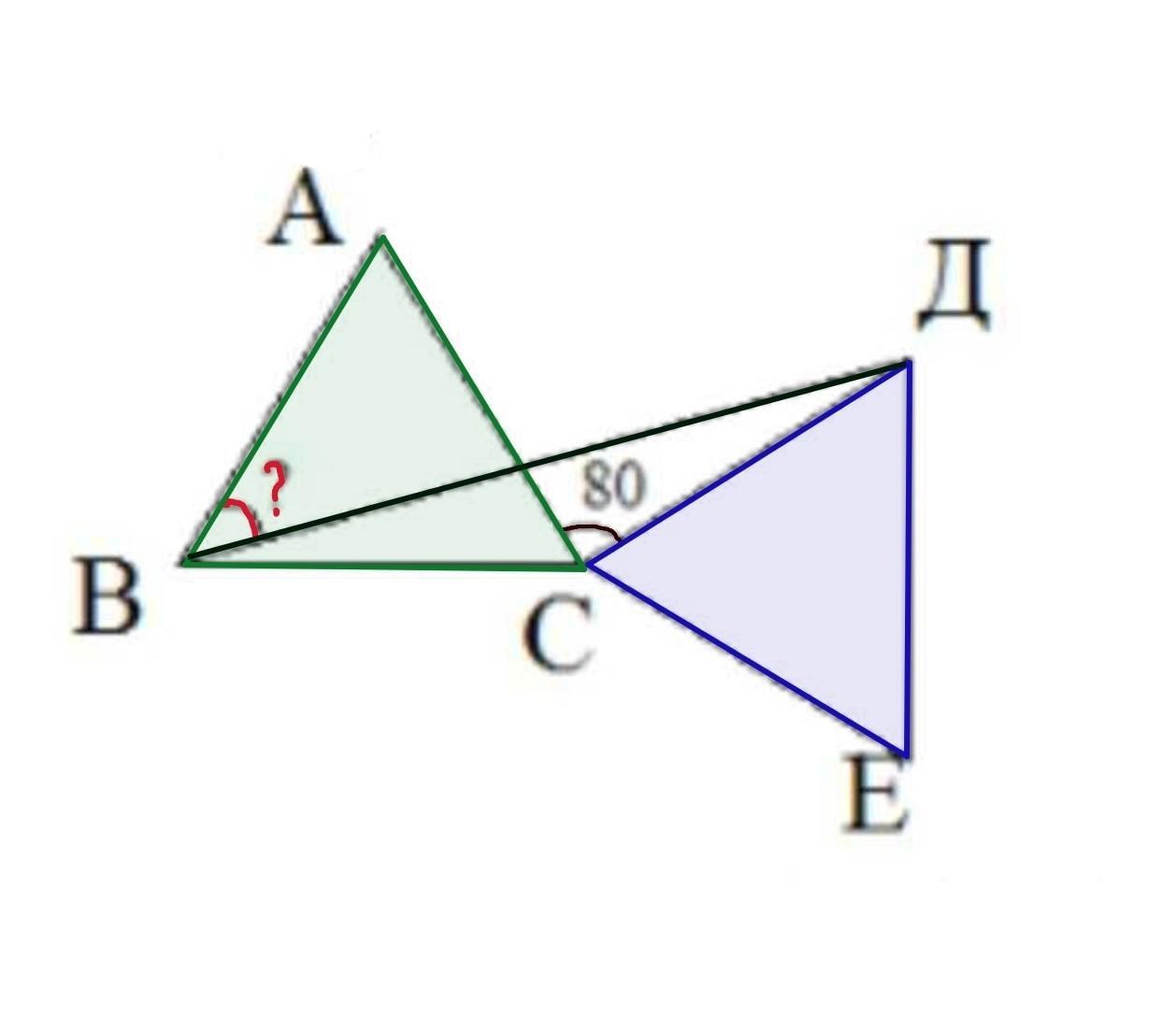
Два однакових рівносторонніх трикутника АВС і СДЕ мають спільну вершину С. Знайдіть ∠ АВД, якщо ∠АСД = 80°.
Дано: △АВС=△СДЕ, АВ=ВС=АС, СД=ДЕ=СЕ, ∠АСД=80°
Знайти: ∠АВД
1.
∠ВСД=∠ВСА+∠АСД - за аксиомою вимірювання кутів.
∠ВСА=60° - як кут рівностороннього трикутника.
∠ВСД=60°+80°=140°
2.
Так як △АВС=△СДЕ, то АВ=ВС=СД=ДЕ=СЕ.
3.
У △ВСД ВС=СД, отже він рівнобедрений з основою ВД.
∠СВД=∠СДВ - як кути при основі рівнобедреного трикутника.
За теоремою про суму кутів трикутника знайдемо їх градусну міру:
∠СВД=∠СДВ=(180°-∠ВСД)÷2=(180°-140°)÷2=20°.
4.
∠АВС=∠АВД+∠СВД,
тоді ∠АВД=∠АВС-∠СВД=60°-20°=40°
#SPJ1
Приложения:
Похожие вопросы
Предмет: ОБЖ,
автор: a04321268
Предмет: Алгебра,
автор: kondratenkoalekseii2
Предмет: Английский язык,
автор: tuleutaevamir67
Предмет: Английский язык,
автор: luba789p47m9p
Предмет: Русский язык,
автор: va1097674