Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Знайти границі послідовностей. n --> ∞
Приложения:
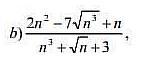
Ответы
Автор ответа:
1
Разделим числитель и знаменатель на старшую степень, здесь это n³.
Похожие вопросы
Предмет: Математика,
автор: hristian388
Предмет: Литература,
автор: svn007
Предмет: Алгебра,
автор: LYAKER
Предмет: Алгебра,
автор: Аноним
Предмет: Другие предметы,
автор: vanakrasinov48