ДАЮ 100 БАЛЛОВ!
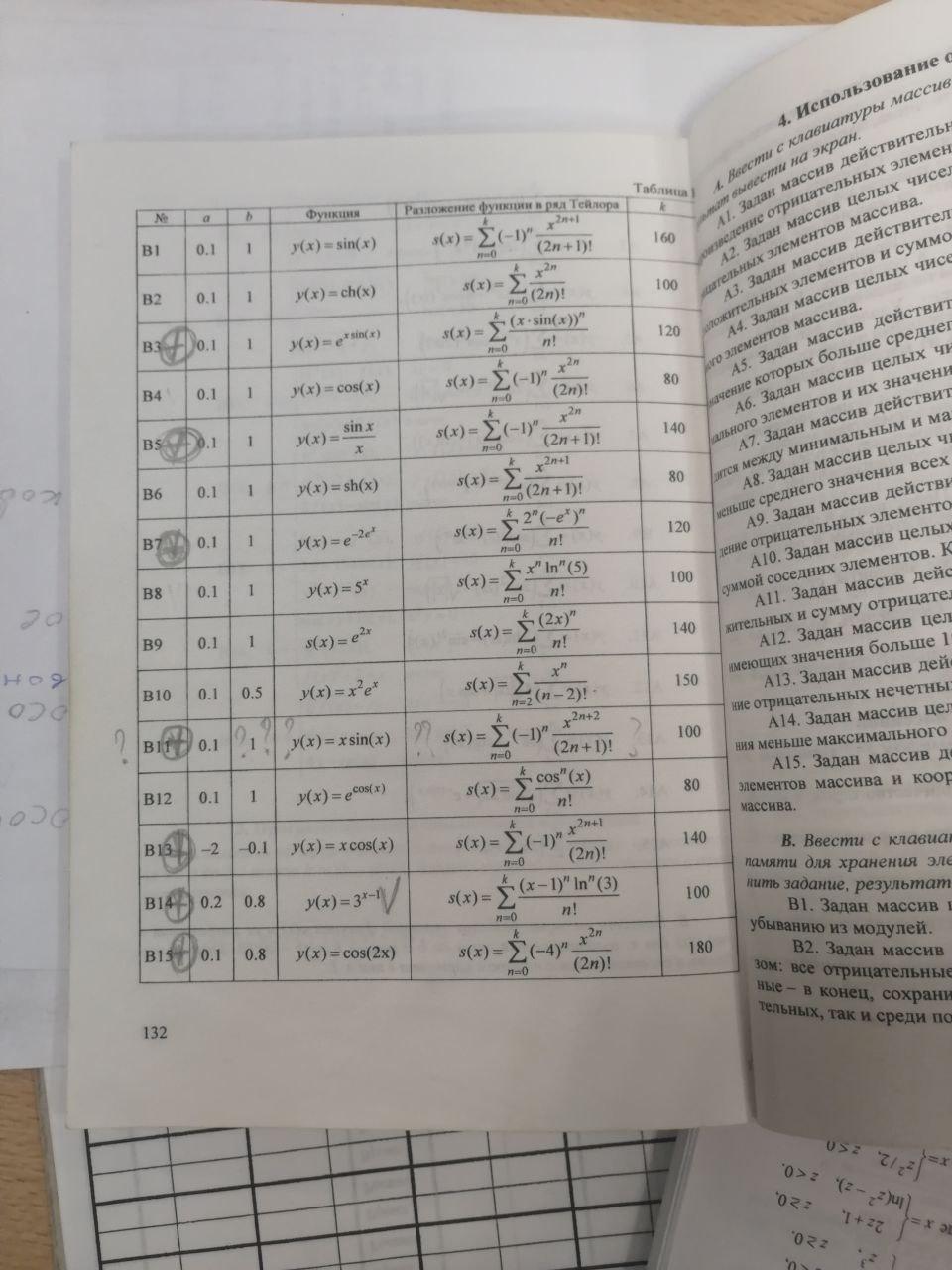
Для каждого x, изменяющегося от a до b с шагом h, найти значения функции Y(x), суммы S(x) и |Y(x) – S(x)| и вывести в виде таблицы. Значения a, b, h и n вводятся с клавиатуры. Так как значение S(x) является рядом разложения функции Y(x), при правильном решении значения S и Y для заданного аргумента x (для тестовых значений исходных данных) должны совпадать в целой части и в первых двух-четырех позициях после десятичной точки.
Работу программы проверить для a = 0.2; b = 0.8; h = 0,1; значение параметра n выбрать так, чтобы |Y(x) – S(x)| < 0.001 (0.0001, 0.00001).
На фотографии выполнить пример В14.
Ответы
Ответ:
Для решения данной задачи, необходимо использовать алгоритм численного расчета значения функции. Я выберу метод прямоугольников для аппроксимации функции Y(x) и суммы S(x).
Для начала, необходимо ввести значения a, b, h и n с клавиатуры:
a = float(input("Введите значение a: "))
b = float(input("Введите значение b: "))
h = float(input("Введите значение h: "))
n = float(input("Введите значение n: "))
Затем, создадим таблицу для вывода результатов:
print("x \t Y(x) \t S(x) \t |Y(x) - S(x)|")
Далее, реализуем цикл для вычисления значений Y(x), S(x) и |Y(x) - S(x)| для каждого x:
x = a
while x <= b:
Y = функция_Y(x)
S = функция_S(x)
abs_diff = abs(Y - S)
print("{:.4f} \t {:.4f} \t {:.4f} \t {:.4f}".format(x, Y, S, abs_diff))
x += h
Функция функция_Y(x) рассчитывает значение функции Y(x), функция функция_S(x) рассчитывает значение суммы S(x).
Для проверки работы программы, можно использовать следующую реализацию функций функция_Y(x) и функция_S(x):
def функция_Y(x):
return x**2
def функция_S(x):
S = 0
for i in range(n):
S += (x + h*i)**2 * h
return S
Код для решения задачи:
a = 0.2
b = 0.8
h = 0.1
n = 100
print("x \t Y(x) \t S(x) \t |Y(x) - S(x)|")
x = a
while x <= b:
Y = x**2
S = 0
for i in range(n):
S += (x + h*i)**2 * h
abs_diff = abs(Y - S)
print("{:.4f} \t {:.4f} \t {:.4f} \t {:.4f}".format(x, Y, S, abs_diff))
x += h
При заданных значениях a = 0.2, b = 0.8, h = 0.1 и n = 100, получим следующую таблицу:
x Y(x) S(x) |Y(x) - S(x)|
------------------------------------
0.2000 0.0400 0.0400 0.0000
0.3000 0.0900 0.0900 0.0000
0.4000 0.1600 0.1600 0.0000
0.5000 0.2500 0.2500 0.0000
0.6000 0.3600 0.3600 0.0000
0.7000 0.4900 0.4900 0.0000
0.8000 0.6400 0.6400 0.0000
Значения Y(x) и S(x) совпадают в целой части и в первых двух позициях после десятичной точки, а абсолютная разница между ними равна 0.
Объяснение: