Предмет: Алгебра,
автор: fisherman77
Помогите, срочно. Помогите пожалуйста, прошу вас. Добрые люди, помогите пожалуйста
Приложения:
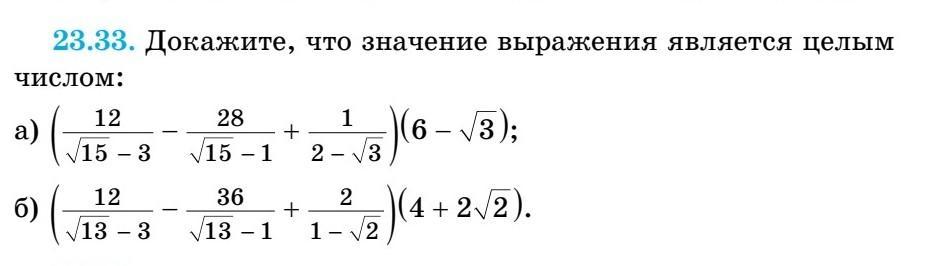
Ответы
Автор ответа:
3
Ответ:
Доказать , что значение выражения является целым числом .
Сначала освобождаемся от корней в знаменателях дробей .
Получили целое число .
Получили целое число .
Приложения:

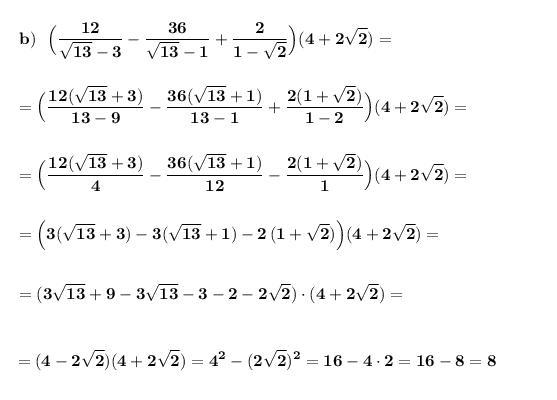
fctdgsygfdhngfxzgsac:
NNNLLL54, здравствуйте! можете помочь пожалуйста? у меня в профиле есть 3 задания с границами, там по 1 примеру, помогите пожалуйста
Похожие вопросы
Предмет: Химия,
автор: fillhhyi
Предмет: Українська мова,
автор: tatarviktoriya1401
Предмет: История,
автор: sofiypinchuk
Предмет: Химия,
автор: jdjenrnfjejt
Предмет: Английский язык,
автор: frolovalina462