Помогите пожалуйста Найти общее решение 12
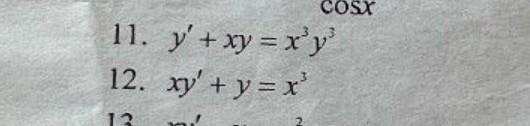
Ответы
Ответ:
Объяснение:
Ответ:
11. 12.
Объяснение:
11. Это уравнение Бернулли. Его можно сразу свести к линейному уравнению с помощью замены
а можно решать так же, как и линейные - с помощью замены y=uv (фактически это метод вариации произвольной постоянной). Пойдем вторым путем.
Подберём ненулевую функцию v(x), обращающую скобку в ноль:
Мы не приписывали произвольную постоянную, так как нас сейчас интересует не общее решение, а одно ненуленое решение. Если эта выкладка показалась не вполне понятной, можете разделить переменные:
Подставляя в уравнение найденное v (при этом скобка обратится в ноль), получаем
12. Это линейное уравнение: его можно решать тем же способом. Но мы решим проще. Заметим, что (xy)'=xy'+y, поэтому уравнение может быть записано в виде
Замечание. Деление на x не приводит к потере решения, поскольку x=0 решением не является.