Помогите пожалуйста Найти общее решение 12
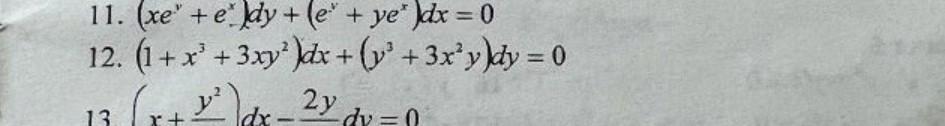
Ответы
Ответ:
Общее решение дифференциального уравнения:
Объяснение:
Найти общее решение дифференциального уравнения:
(1 + х³ + 3ху²)dx + (y³ + 3x²y)dy = 0
1. Определим вид уравнения.
Найдем частную производную по х первого слагаемого и по у второго слагаемого:
- производные равны, значит, уравнение является уравнением в полных дифференциалах вида:
2. Запишем систему уравнений:
3. Проинтегрируем первое уравнение по х (y - const):
4. F продифференцируем по y:
Приравняем ко второму уравнению системы:
5. Проинтегрируем и найдем φ(у):
6. Подставим φ(у) в (1):
Ответ:
11. 12.
Объяснение:
Конечно, это уравнения в полных дифференциалах. Хочу показать, как их можно решать проще.
11.
12.