Алгебра 11клас,85 балів .
Завдання : 3,4,5,8,10
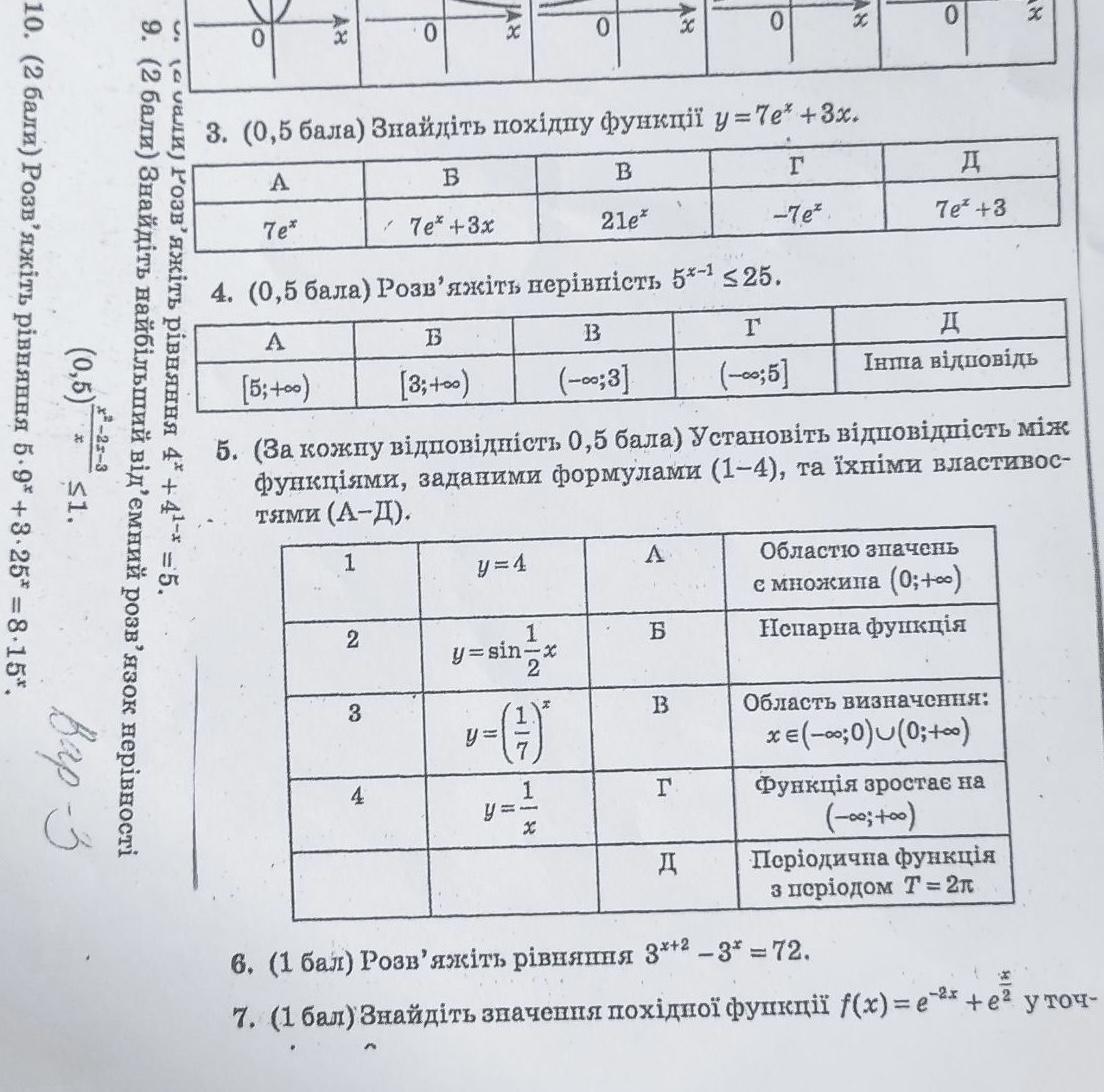
Ответы
Ответ:
удачи!
Объяснение:
3. в
4. в
5.
1 - Д (Функція y = 4 зростає на всьому діапазоні (-∞, +∞), та не є періодичною.)
2 - Б (Областью значень функції y = sin(1/2 * x) є множина [-1, 1], і вона є непарною функцією.)
3 - A (Функція y = (1/7)^x має область визначення в діапазоні x від (-∞, +∞) та область значень (0, +∞).)
4 - Г (Функція y = 1/x зростає на всьому діапазоні (-∞, +∞).)
8.Для розв'язання рівняння 4^x + 4^(1 - x) = 5, спробуйте скористатися підстановкою, щоб спростити рівняння:
Позначимо 4^x як y. Тоді ми отримаємо:
y + 4 / y = 5
Ми можемо перемножити обидві сторони на y, щоб позбавитися від дробів:
y^2 + 4 = 5y
Тепер перенесемо всі члени на одну сторону та спростимо:
y^2 - 5y + 4 = 0
Далі ми можемо розв'язати це квадратне рівняння:
(y - 4)(y - 1) = 0
З цього розв'язку маємо два можливі значення для y:
1) y - 4 = 0, тобто y = 4
2) y - 1 = 0, тобто y = 1
Тепер ми можемо повернутися до виразу, з яким ми працювали:
4^x = 4 або 4^x = 1
Для першого випадку, x = 1, оскільки 4^1 = 4.
Для другого випадку, x = 0, оскільки 4^0 = 1.
Отже, рівняння має два розв'язки: x = 1 і x = 0.
10.Для розв'язання цього рівняння використовуємо властивості степеневих функцій та деякі алгебраїчні перетворення.
Спочатку помітимо, що 25 = 5^2 та 15 = 3 * 5. Тепер можемо виразити числа 25 та 15 через 5 та 3:
5 * 9^x + 3 * (5^2)^x = 8 * (3 * 5)^x
Далі спростимо вирази, використовуючи властивості степеневих функцій:
5 * 3^(2x) + 3 * 5^(2x) = 8 * 3^x * 5^x
Тепер зведемо всі члени з 5^x на одну сторону рівності, а всі члени з 3^x на іншу сторону:
5 * 3^(2x) - 8 * 3^x * 5^x + 3 * 5^(2x) = 0
Звернімо увагу, що всі три члени рівняння мають 5^(2x) та 3^x, тому ми можемо використовувати підстановку, щоб спростити рівняння. Позначимо 3^x як y:
5y^2 - 8y * 5^(2x) + 3 * 5^(2x) = 0
Тепер ми отримали квадратне рівняння відносно y:
5y^2 - 8y * 5^(2x) + 3 * 5^(2x) = 0
Можемо використовувати дискримінант для знаходження розв'язків цього квадратного рівняння:
D = (8 * 5^(2x))^2 - 4 * 5 * 3 * 5^(2x)
D = 64 * 25^(2x) - 60 * 25^(2x)
D = 4 * 25^(2x)
Тепер знайдемо значення y за допомогою дискримінанту:
y = (-b ± √D) / (2a)
y = (-(-8 * 5^(2x)) ± √(4 * 25^(2x))) / (2 * 5)
y = (8 * 5^(2x) ± 2 * 25^x) / 10
y = (4 * 5^(2x) ± 25^x)
Зараз можемо повернутися до виразу, в якому ми позначили y як 3^x:
3^x = 4 * 5^(2x) ± 25^x
Тепер ми маємо два можливі випадки, один для кожного знаку ±:
1. 3^x = 4 * 5^(2x) + 25^x
2. 3^x = 4 * 5^(2x) - 25^x
Обидва ці рівняння можна розв'язати, але це вимагає складних алгебраїчних обчислень. Рівняння має багато розв'язків, і їхні значення будуть складними числами. Я б рекомендував використовувати обчислювальний програмний засіб для числового розв'язання цих рівнянь.