Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Знайти границі послідовностей. Будь ласка допоможіть.
Приложения:
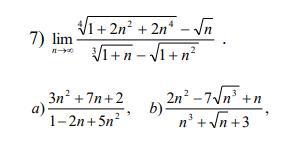
Ответы
Автор ответа:
2
Ответ:
Найдём пределы , поделив числитель и знаменатель на старшую степень .
Приложения:
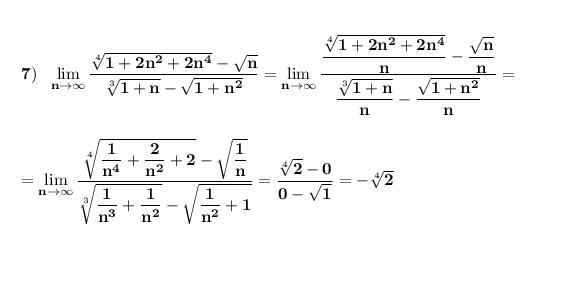
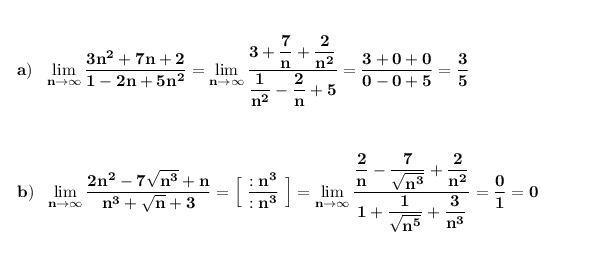
fctdgsygfdhngfxzgsac:
спасибо большое)
Похожие вопросы
Предмет: Українська мова,
автор: polina171719
Предмет: Українська мова,
автор: alyonalevterova
Предмет: Українська мова,
автор: Аноним
Предмет: Физика,
автор: lika7266
Предмет: Химия,
автор: z4il7777