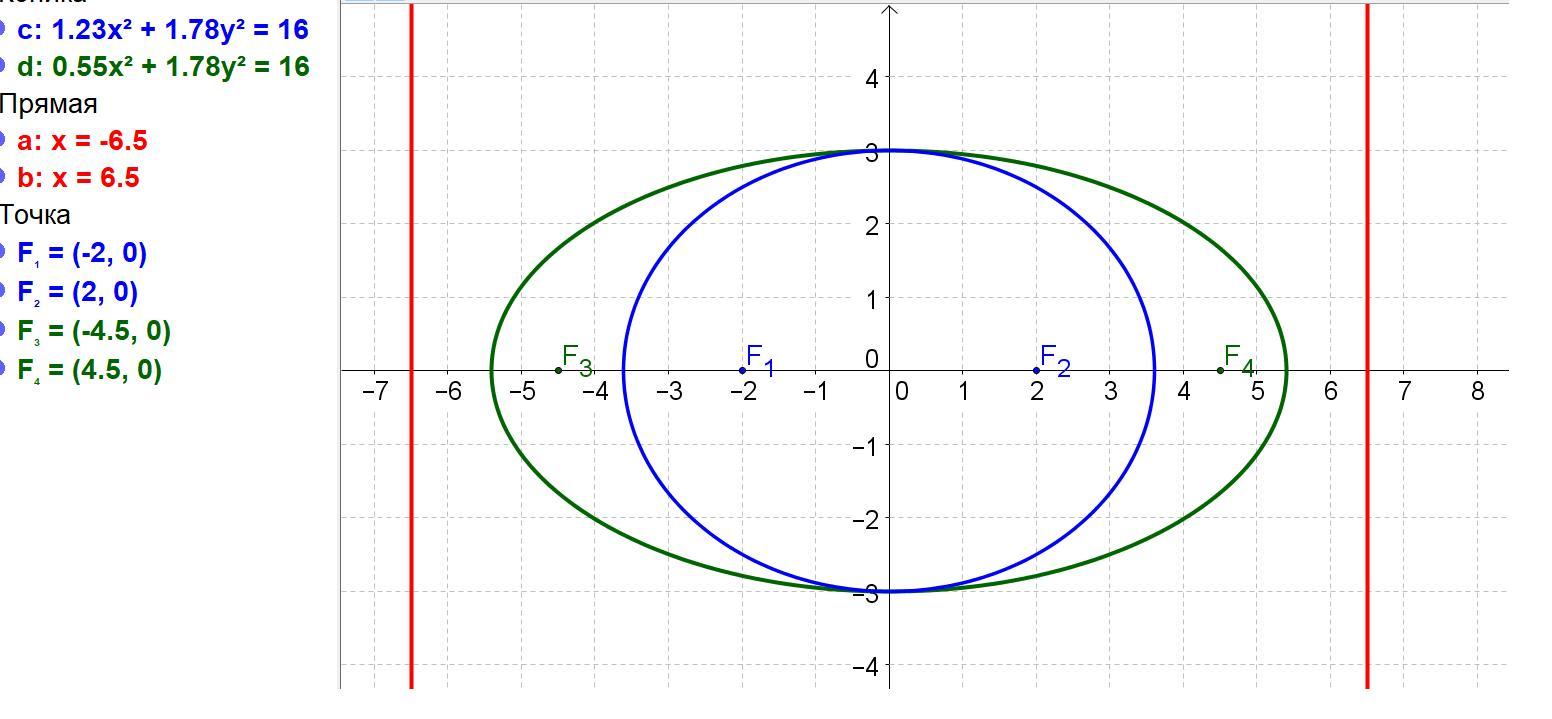
Составьте уравнение эллипса если его малая ось равна 6, а расстояние между директрисами равен 13
Ответы
Составьте уравнение эллипса если его малая ось равна 6, а расстояние между директрисами равен 13.
Если эллипс определен уравнением (x²/a²) + (y²/b²) = 1 и , то прямые x = -a/e, x = a/e называются директрисами эллипса.
Расстояние от центра до директрисы – это половина заданной величины 13.
То есть х = 13/2.
Прямые x = +-(13/2) служат директрисами эллипса, малая ось которого равна 2b = 6..
Малая полуось эллипса b = 6/2 = 3. . Чтобы составить уравнение эллипса нужно знать большую полуось. Имеем: x = a/e, e = c/a. Следовательно, x = a²/c . Так как x = (13/2) , то a² = (13/2)c. Учитывая, что c² = a² - 3² , получим, что величина c удовлетворяет уравнению
c² - (13/2)c + 9 = 0 или с целыми коэффициентами 2c² - 13c + 18 = 0.
Ищем дискриминант:
D=(-13)^2-4*2*18=169-4*2*18=169-8*18=169-144=25;
Дискриминант больше 0, уравнение имеет 2 корня:
c_1=(√25-(-13))/(2*2)=(5-(-13))/(2*2)=(5+13)/(2*2)=18/(2*2)=18/4=4.5;
c_2=(-√25-(-13))/(2*2)=(-5-(-13))/(2*2)=(-5+13)/(2*2)=8/(2*2)=8/4=2.
Получили 2 значения фокусного расстояния.
Значит, имеем 2 величины большей полуоси.
а²(1) = (13/2)*4,5 = (13/2)*(9/2)) = (117/4).
а²(2) = (13/2)*2 = 13.
Отсюда получаем 2 ответа:
(x²/(117/4)) + (y²/9) = 1
(x²/13) + (y²/9) = 1