Предмет: Алгебра,
автор: person4884
Можете,пожалуйста, решить уравнение
Приложения:
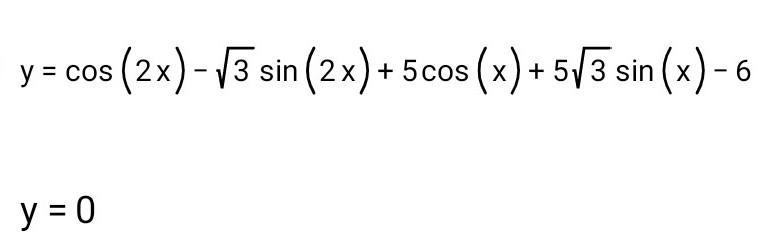
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Мы воспользовались следующими формулами:
masha01021:
здравствуйте, извините, можете помочь пожалуйста
Похожие вопросы
Предмет: Русский язык,
автор: m78214145
Предмет: Кыргыз тили,
автор: Herrrrr
Предмет: Математика,
автор: thfttvtgfdhddgh
Предмет: Қазақ тiлi,
автор: oksanah2
Предмет: Қазақ тiлi,
автор: eazizova971