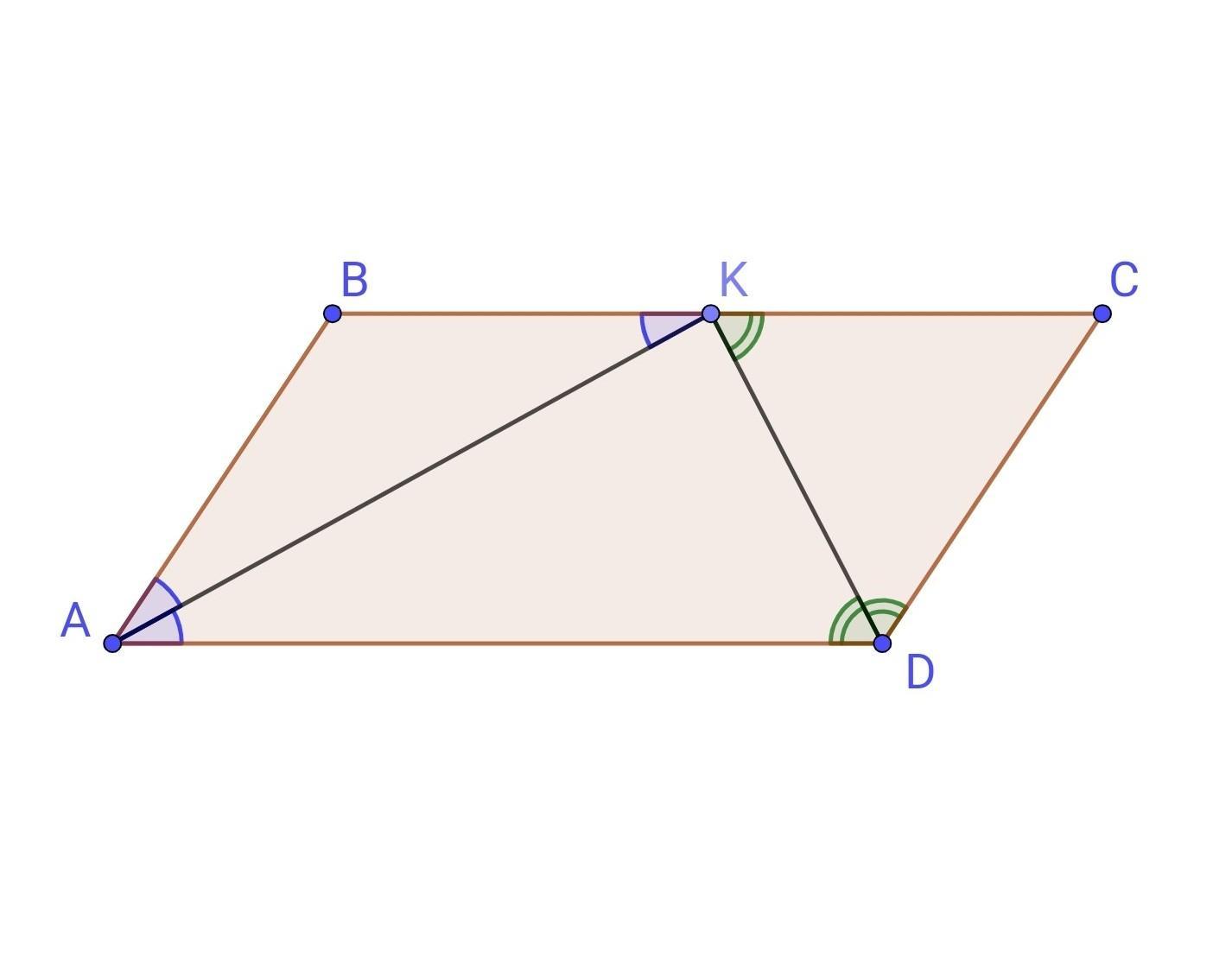
Знайдіть периметр паралелограма ABCD, якщо його менша сторона дорівнює 5 см, а бісектриси кутів А і D перетинаються в точці К., яка лежить на стороні ВС. Знайдіть міру Кута AKD.
допоможіть
Ответы
Ответ:
Периметр паралелограма дорівнює 30 см.
∠АКD=90°.
Объяснение:
Знайдіть периметр паралелограма ABCD, якщо його менша сторона дорівнює 5 см, а бісектриси кутів А і D перетинаються в точці К, яка лежить на стороні ВС. Знайдіть міру Кута AKD.
Дано: ABCD - паралелограм, AB=CD=5 см (протилежні сторони паралелограма), AK - бісектриса кута А, DK - бісектриса кута D. AK∩DK=K,
K ∈ BC.
Знайти: P(ABCD), ∠AKD.
Розв'язання
1.
∠KAD=∠AKB - як внутрішні різносторонні кути при перетині паралельних прямих AD і BC січною AK.
∠KAD=∠BAK - за умовою.
Отже, ∠AKB=∠BAК, тому за ознакою рівнобедреного трикутника: △ABK - рівнобедрений з основою AK.
AB=BK=5(см) як бічні сторони рівнобедреного трикутника.
2.
∠ADK=∠DKC - як внутрішні різносторонні кути при перетині паралельних прямих AD і BC січною DK.
∠ADK=∠KDC - за умовою.
Отже, ∠DKC=∠KDC, тому за ознакою рівнобедреного трикутника: △KCD - рівнобедрений з основою KD.
CD=KC=5(см) як бічні сторони рівнобедреного трикутника.
3.
За аксиомою вимірювання відрізків отримаємо:
BC=BK+KC=5+5= 10 (см)
4.
Знайдемо периметр паралелограма, як подвоєну суму двох сусідніх сторін:
Р(ABCD)=2(AB+BC) = 2(5+10)=2•15= 30 (см)
5.
∠A+∠D=180° - як сусідні кути паралелограма.
За означенням бісектриси кута маємо:
∠KAD = ½ • ∠A
∠KDA = ½ • ∠D
Тоді:
∠KAD + ∠KDA = ½ • ∠A + ½ • ∠D =
= ½ • (∠A + ∠D) = ½ • 180° = 90°.
За теоремою про суму кутів трикутника знайдемо кут AKD трикутника AKD:
∠KAD + ∠KDA + ∠AKD = 180°
∠AKD = 180° - (∠KAD+∠KDA) = 180° - 90° = 90°.
#SPJ1