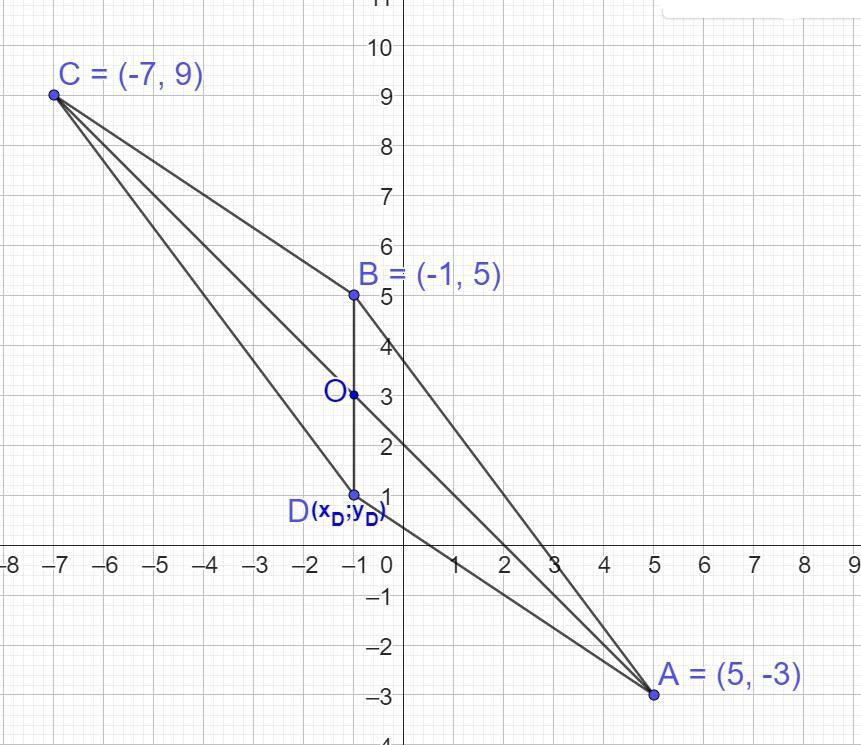
Вiдомi координати трьох вершин паралелограма ABCD: A (5;-3), В (-1;5), С (-7;9). У якій координатній чверті розташована четверта вершина паралелограма?
Ответы
Ответ:
Вершина D(-1; 1 ) розташована в ІІ координатній чверті.
Объяснение:
Вiдомi координати трьох вершин паралелограма ABCD: A (5;-3), В (-1;5), С (-7;9). У якій координатній чверті розташована четверта вершина паралелограма?
Для відшукання четвертої вершини скористаємося властивістю про те, що у паралелограма ABCD діагоналі AC і BD в точці перетину (О) діляться навпіл:
AО=ОC, BО=ОD.
Спочатку знайдемо координати центра О - середини відрізка (діагоналі) AC за відомими координатами:
Отримали O(-1; 3) - координати точки перетину діагоналей AC і BD.
Із умови, що BO=OD складаємо рівняння для знаходження координати точки D і розв'язуємо:
D(-1; 1 ) - шукана вершина.
- якщо точка належить другій координатній чверті, тоді x<0; y>0.
Так як абсциса точки D: -1 <0, а ордината 1 > 0, то точка D розташована в ІІ координатній чверті.
#SPJ1