Предмет: Геометрия,
автор: arinazarin
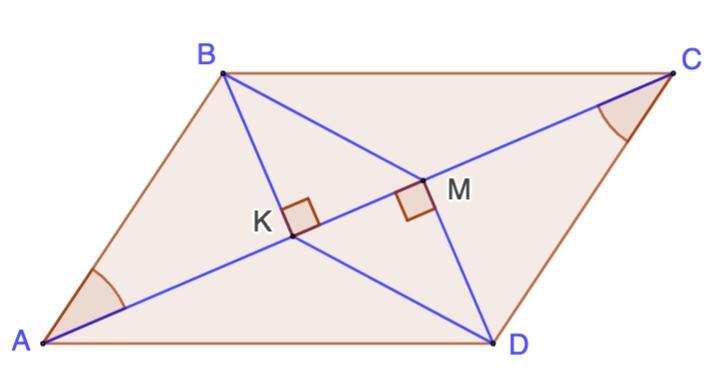
В параллелограмме ABCD смежные стороны не равны. К диагонали, соединяющей острые углы параллелограмма проведены две высоты ВК и MD. Доказать, что MBKD - параллелограмм.
СРОЧНО!!!!
Ответы
Автор ответа:
2
Ответ:
Доказано, что MBKD - параллелограмм.
Объяснение:
В параллелограмме ABCD смежные стороны не равны. К диагонали, соединяющей острые углы параллелограмма проведены две высоты ВК и MD. Доказать, что MBKD - параллелограмм.
Дано: ABCD - параллелограмм;
АС - диагональ;
ВК ⊥ АС; MD ⊥ AC.
Доказать: MBKD - параллелограмм;
Доказательство:
1. Рассмотрим ΔАВК и ΔСDM - прямоугольные.
- Противоположные стороны параллелограмма равны.
⇒ АВ = CD
∠ BAK = ∠DCM (накрест лежащие при АВ || CD и секущей АС)
⇒ ΔАВК = ΔСDM (по гипотенузе и острому углу)
⇒ ВК = MD (как соответственные элементы)
2. ВК ⊥ АС; MD ⊥ AC.
- Если две прямые перпендикулярны третьей, то они параллельны между собой.
⇒ ВК || MD
3. Рассмотрим MBKD.
ВК = MD; ВК || MD.
- Если две противоположные стороны четырехугольника равны и параллельны, то этот четырехугольник - параллелограмм.
⇒ MBKD - параллелограмм.
#SPJ1
Приложения:
fctdgsygfdhngfxzgsac:
natalyabryukhova, здравствуйте! можете помочь пожалуйста? у меня в профиле 5 вопросов по векторам, прошу помогите
natalyabryukhova, здравствуйте! можете помочь пожалуйста? у меня в профиле есть 2 задания с границами последовательностей, прошу помогите
Похожие вопросы
Предмет: Литература,
автор: trummaksim1
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: akupovamadina
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: neckrasovas