Предмет: Алгебра,
автор: drygind244
Помогите пожалуйста срочно!!!
Приложения:
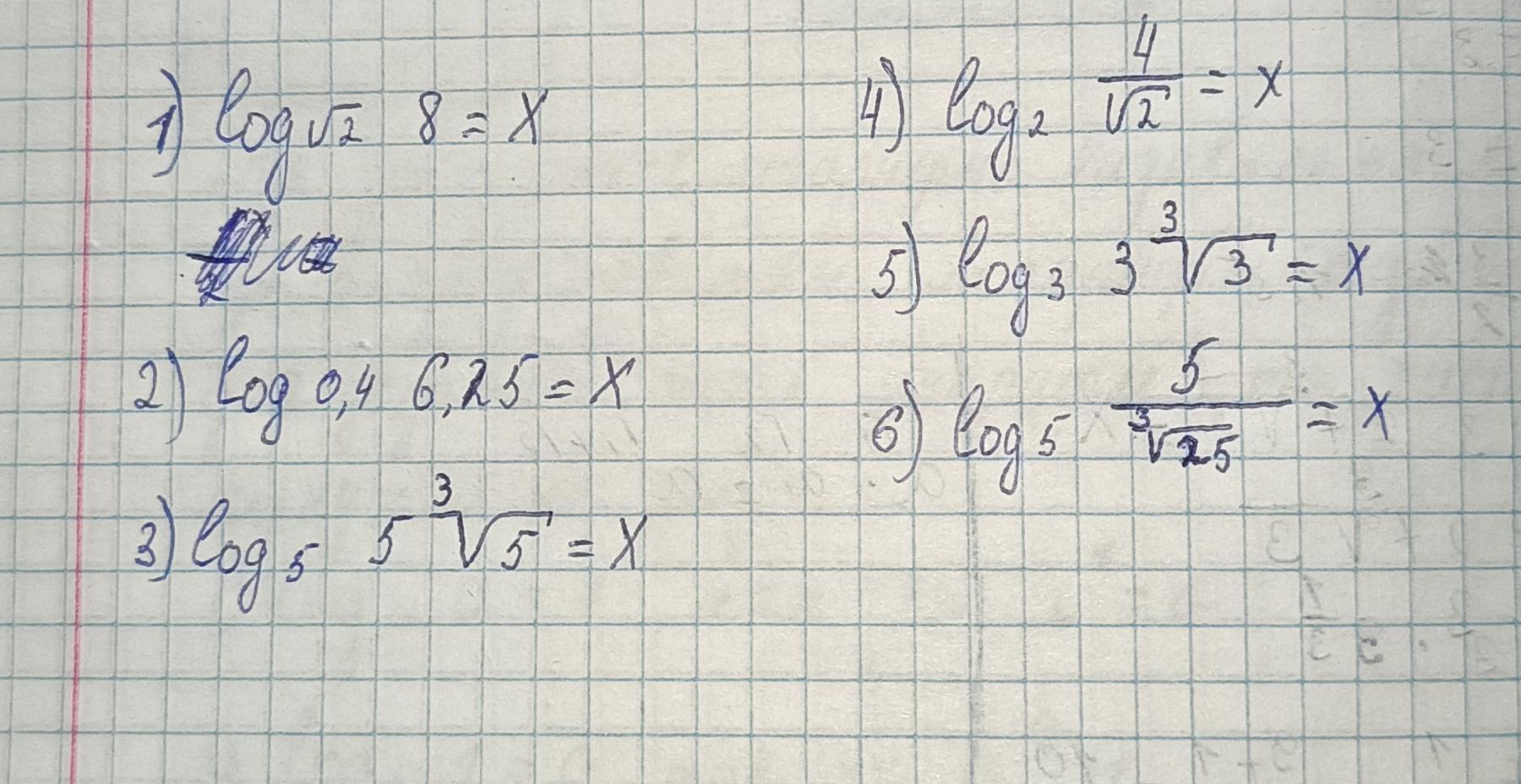
Ответы
Автор ответа:
0
Ответ:
Решить уравнение .
По определению логарифма их равенства
, следует , что
.
atlantic0cean:
https://znanija.com/task/53653195
Похожие вопросы
Предмет: Химия,
автор: alishckamalishcka
Предмет: История,
автор: bekzatberkenov2
Предмет: География,
автор: tanyashapik
Предмет: Физкультура и спорт,
автор: Аноним
Предмет: Литература,
автор: sofiasagatdinowa