ОЧЕНЬ СРОЧНО
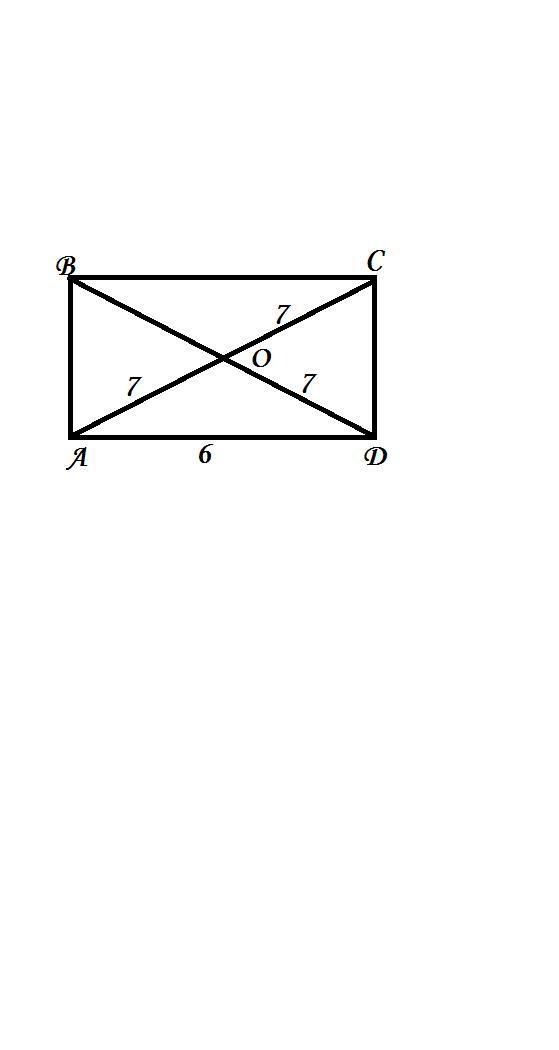
О - точка перетину діагоналей прямокутника ABCD, AD = 6 см, периметр трикутника AOD дорівнює 20 см. Знайдіть АС
Ответы
Відповідь:
ABCD дорівнює 7 см
Пояснення:
Ми можемо використовувати властивості прямокутника та трикутника AOD, а також властивості діагоналей, щоб знайти довжину сторони AC прямокутника ABCD.
Оскільки AD - діагональ прямокутника, то точка О - середина діагоналі AC. Тобто AO = OC.
Периметр трикутника AOD дорівнює сумі довжини сторін AD, AO і OD. Маємо:
20 см = AD + AO + OD
20 см = 6 см + AO + OD
AO + OD = 20 см - 6 см = 14 см
Оскільки AO = OC (за властивістю серединної лінії діагоналі), то ми можемо записати:
AO = OC = 1/2 * AC
Підставимо це у нашу попередню рівність:
1/2 * AC + OD = 14 см
Також ми знаємо, що OD - це половина діагоналі BD, а BD - це інша діагональ прямокутника, тобто BD = AC. Таким чином, OD = 1/2 * AC.
Підставимо це значення в рівняння:
1/2 * AC + 1/2 * AC = 14 см
Спростимо рівняння:
AC + AC = 14 см
2AC = 14 см
Поділимо обидві сторони на 2:
AC = 14 см / 2
AC = 7 см
Отже, довжина сторони AC прямокутника ABCD дорівнює 7 см.
Ответ:
14 см.
Объяснение:
Дано: прямокутник ABCD, AD = 6 см, Р(AOD)=20 см. АС -?
Діагоналі прямокутника рівні і точкою перетину діляться навпіл.
ΔАОD - рівнобедрений, АО=ОD=(20-6):2=7 см.
АС=АО+СО=7+7=14 см.