Question

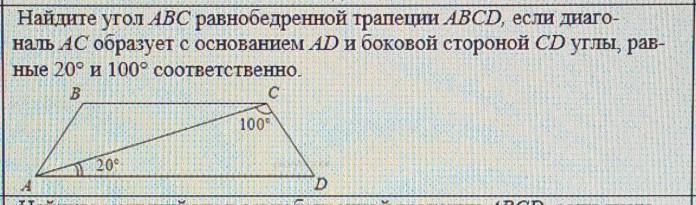
Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.​

Answer 1

Уравнение суммы углов в трапеции ABCD:

Угол АBC + Угол ACD + Угол BCD + Угол CDA = 360°

Учитывая, что трапеция ABCD равнобедренная, то угол ABC равен углу BCD.

По условию, угол ACD = 20° и угол CDA = 100°.

Углы ABC и BCD можно обозначить буквой "х".

Уравнение примет вид:

х + 20° + х + х + 100° = 360°

3х + 120° = 360°

3х = 240°

х = 80°

Таким образом, угол ABC (или BCD) равен 80°.

Answer 2

Ответ:

угол ABC равен 120 градусов.

Объяснение:

Из треугольника ACD находим угол CDA:

Сумма углов в треугольнике равна 180 градусов

180°-20°-100°=60° (угол CDA)

Угол АСВ равен углу CAD (накрест лежащие углы)

Угол АСВ=20°

Угол ABC равен углу BCD, потому что трапеция равнобедренная. Найдем угол BCD:

20°+100°=120°