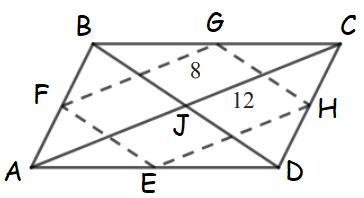
Длины диагоналей параллелограмма равны 8 и 12. Средние точки его ребер были последовательно соединены, чтобы получить меньший четырехугольник.
a) Определите, по крайней мере, два различных треугольника на рисунке, которые имеют среднюю линию! Назовите эти треугольники! Не забудьте обосновать, что треугольники разные!
b) Вычислите периметр наименьшего четырехугольника!
c) Запишите в общем виде зависимость между периметром P наименьшего четырехугольника и длинами d1 и d2 диагоналей параллелограмма!
Ответы
Ответ:a) Для того чтобы определить два различных треугольника, имеющих среднюю линию, давайте рассмотрим, как диагонали параллелограмма делят его на треугольники. Диагонали разбивают параллелограмм на четыре треугольника: два больших и два меньших. Для нахождения двух треугольников, имеющих среднюю линию, давайте соединим средние точки ребер, как указано в условии.
Первый треугольник - это тот, который образуется соединением средних точек боковых сторон параллелограмма. Давайте назовем его "треугольник ABC", где A и C - средние точки двух противоположных сторон, а B - точка, где диагонали пересекаются.
Второй треугольник - это тот, который образуется соединением средних точек других двух сторон параллелограмма. Давайте назовем его "треугольник ACD", где A и C - те же средние точки, что и в первом треугольнике, а D - точка пересечения других двух диагоналей.
b) Для нахождения периметра наименьшего четырехугольника, нужно сложить длины его всех четырех сторон. Эти стороны - это отрезки AB, BC, CD и DA, которые соответствуют половинам сторон параллелограмма. Таким образом, периметр P наименьшего четырехугольника равен:
P = AB + BC + CD + DA = (1/2)d1 + (1/2)d2 + (1/2)d1 + (1/2)d2 = (d1 + d2).
c) Зависимость между периметром P наименьшего четырехугольника и длинами диагоналей d1 и d2 параллелограмма может быть записана следующим образом:
P = d1 + d2.
Это уравнение показывает, что периметр наименьшего четырехугольника равен сумме длин обеих диагоналей параллелограмма.
Пошаговое объяснение:
ОТВЕТ:А. Для того чтобы определить два различных треугольника, имеющих среднюю линию, давайте рассмотрим, как диагонали параллелограмма делят его на треугольники. Диагонали разбивают параллелограмм на четыре треугольника: два больших и два меньших. Для нахождения двух треугольников, имеющих среднюю линию, давайте соединим средние точки ребер, как указано в условии.
Первый треугольник - это тот, который образуется соединением средних точек боковых сторон параллелограмма. Давайте назовем его "треугольник ABC", где A и C - средние точки двух противоположных сторон, а B - точка, где диагонали пересекаются.
Второй треугольник - это тот, который образуется соединением средних точек других двух сторон параллелограмма. Давайте назовем его "треугольник ACD", где A и C - те же средние точки, что и в первом треугольнике, а D - точка пересечения других двух диагоналей.
b) Для нахождения периметра наименьшего четырехугольника, нужно сложить длины его всех четырех сторон. Эти стороны - это отрезки AB, BC, CD и DA, которые соответствуют половинам сторон параллелограмма. Таким образом, периметр P наименьшего четырехугольника равен:
P = AB + BC + CD + DA = (1/2)d1 + (1/2)d2 + (1/2)d1 + (1/2)d2 = (d1 + d2).
С) Зависимость между периметром P наименьшего четырехугольника и длинами диагоналей d1 и d2 параллелограмма может быть записана следующим образом:
P = d1 + d2.
Это уравнение показывает, что периметр наименьшего четырехугольника равен сумме длин обеих диагоналей параллелогрпараллелограмма.
Сделай лучшым ответ!!!