Question

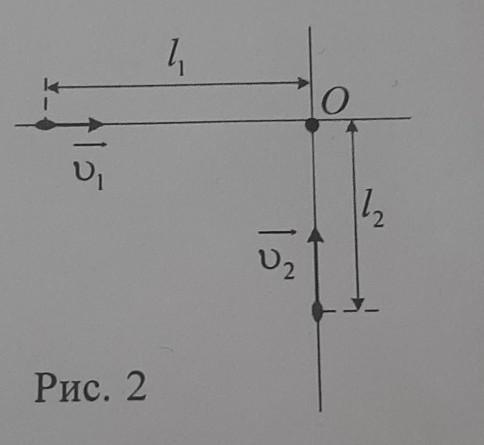
3. Два катера ДВИЖУТСЯ по озеру по взаимно перпендикулярным прямым, пересекающимся в точке О (рис. 2). Модуль скорости равномерного движения первого катера U, = 54 катера КМ V₂ = 72 Ч км Определите Ч второго минимальное расстояние, на котором проплыли друг от друга катера, если в момент времени, когда первому катеру осталось проплыть до точки О расстояние 4=400 м, второй находился о точки О на расстоянии 4, =300 м.​ Прошу я на олимпиаде сижу

Answer 1

Для визуализации рассмотрим два катера, движущихся по перпендикулярным направлениям. Пусть первый катер движется по горизонтали с скоростью \( U_1 = 54 \) км/ч, а второй катер движется по вертикали с скоростью \( V_2 = 72 \) км/ч.

В начальный момент времени, когда до точки О первому катеру осталось 400 м, а второй катер находился на расстоянии 300 м от точки О, можно построить прямоугольный треугольник, где катера находятся на катетах.

После прохождения одного и того же промежутка времени \( t \) первый катер пройдёт расстояние \( 54t \) км (или \( 54000t \) м), а второй катер пройдёт \( 72t \) км (или \( 72000t \) м).

После этого времени \( t \) новые расстояния до точки О будут равны:

1) Для первого катера: \( 400 - 54000t \) м
2) Для второго катера: \( 300 - 72000t \) м

Теперь, расстояние между катерами будет гипотенузой прямоугольного треугольника, где катеты равны измененным расстояниям до точки О.

Расстояние между катерами \( d(t) \) в зависимости от времени \( t \):

\[ d(t) = \sqrt{(400 - 54000t)^2 + (300 - 72000t)^2} \]

Для нахождения минимального расстояния между катерами, необходимо найти минимум функции \( d(t) \). Для этого можно взять производную и приравнять её к нулю.

Однако, в данной задаче, учитывая начальные условия и скорости катеров, можно сказать, что минимальное расстояние будет достигнуто, когда первый катер достигнет точки О, а второй катер будет на 300 м - \( 72000t \) от точки О.

Подставляя \( 400 - 54000t = 0 \), находим \( t = \frac{400}{54000} = \frac{1}{135} \) часа.

Тогда, расстояние, которое пройдет второй катер за это время: \( \frac{1}{135} \times 72000 = 533.33 \) м.

Таким образом, когда первый катер достигнет точки О, второй катер будет на \( 300 + 533.33 = 833.33 \) м от точки О.

Теперь, используя Пифагорову теорему, найдем гипотенузу (расстояние между катерами):

\[ d = \sqrt{400^2 + 833.33^2} \]

\[ d \approx 930 \] м.

Минимальное расстояние, на котором проплыли друг от друга катера, равно примерно 930 метров.