Помогите пожалуйста очень срочно

Ответы
Ответ:
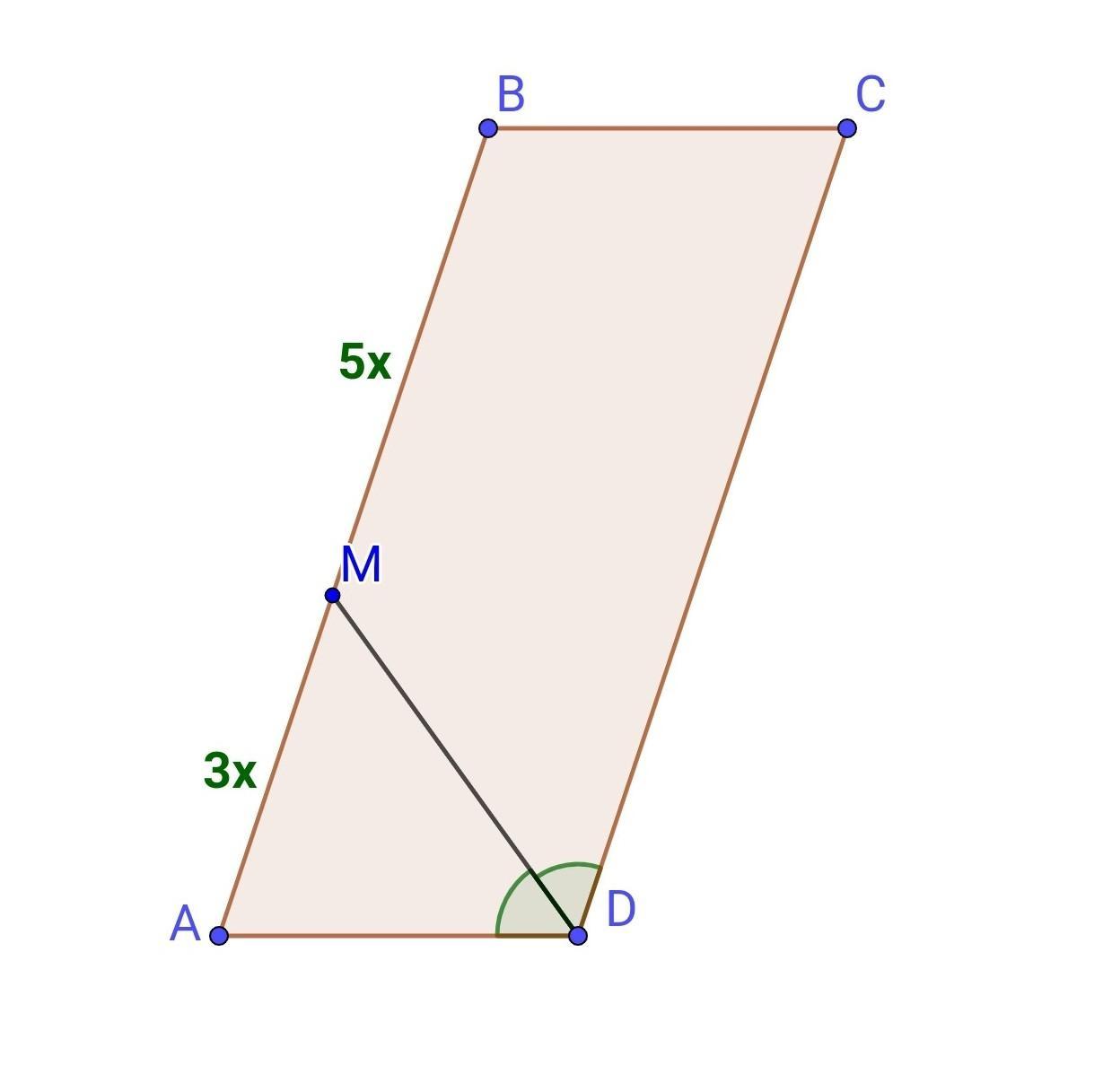
Сторони паралелограма: AB=CD=48 см, AD=BC=18 см
Объяснение:
Бісектриса кута D паралелограма ABCD ділить сторону AB на відрізки AM і МВ так, що АМ:МВ=3:5.Знайдіть сторони паралелограма, якщо його периметр дорівнює 132см.
- Паралелограмом називають чотирикутник у якого протилежні сторони попарно паралельні.
- У паралелограмі протилежні сторони рівні.
Дано: ABCD - паралелограм, AB||CD, BC||AD, AB=CD, BC=AD. DM - бісектриса кута D. DM∩AB=M, AM:MB=3:5, P(ABCD)=132 см
Знайти: АВ, BC, CD, AD.
РОЗВ'ЯЗАННЯ
1.
Нехай AM=3х, а МВ=5х, де х - коефіцієнт пропорційності.
Тоді за аксиомою вимірювання відрізків отримаємо:
AB=AM+MD=3х+5х=8х.
2.
- ∠MDC=∠ADМ - за умовою (за означенням бісектриси кута)
- ∠MDC=∠AMD - як внутрішні різносторонні кути при перетині паралельних прямих AB і CD січною MD.
Отже ∠ADM=∠AMD, тому за ознакою рівнобедреного трикутника: △AMD - рівнобедрений з основою MD.
AD=АМ=3х - як бічні сторони рівнобедреного трикутника.
3.
- Периметр паралелограма дорівнює подвоєної сумі двох його сусідніх сторін.
Р(ABCD)=2•(AB+AD)
Розв'яжемо рівняння:
2•(8х+3х)=132
11х=132:2
11х=66
х=6
Отже, AB=CD=8•6=48(см), AD=BC=3•6=18(см)
#SPJ1