Предмет: Алгебра,
автор: miselgadzieva181
2. Тепе-тендiктi далелде:
/8 + 4√3 = √6 +√2.
Приложения:

Ответы
Автор ответа:
0
Ответ:
Доказать , что .
Запишем подкоренное выражение в виде квадрата другого выражения .
Применим формулу .
Приложения:
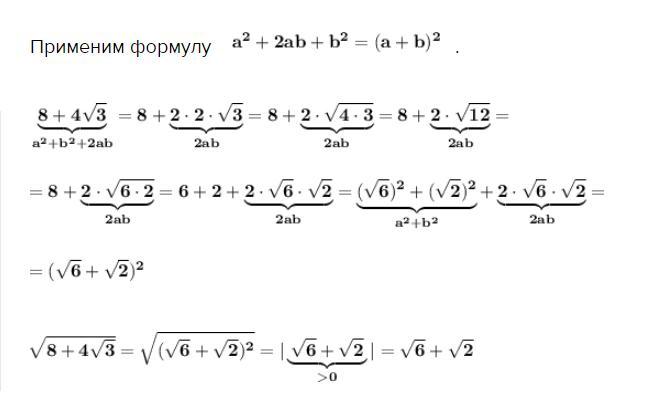
посмотрите этот вопрос
Похожие вопросы
Предмет: Русский язык,
автор: Omina555
Предмет: Українська мова,
автор: nelyakudlovska
Предмет: Алгебра,
автор: alenakitaeva78
Предмет: Алгебра,
автор: tokarevnikita837
Предмет: Алгебра,
автор: helpme932
https://znanija.com/task/53646724?utm_source=android&utm_medium=share&utm_campaign=question