Предмет: Алгебра,
автор: kamenkovaanastasia95
Допоможіть розв'язати рівняння 1і2 не треба
Приложения:
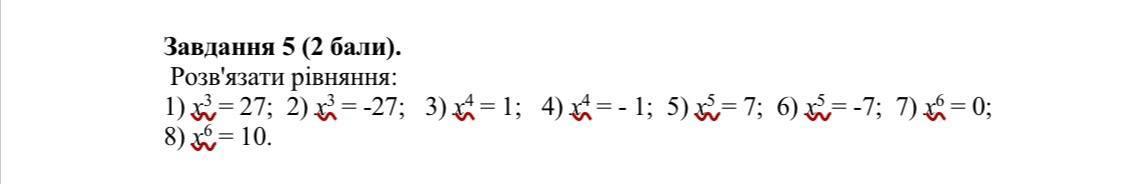
Ответы
Автор ответа:
1
Ответ:
Решить уравнения .
1) Используем формулу разности квадратов .
Можно решить так :
Сумма неотрицательного выражения , , и положительного ,
, даёт положительное выражение , но не 0 .
Приложения:

Похожие вопросы
Предмет: Математика,
автор: KOTIKFelix1
Предмет: История,
автор: anvarbihajitova
Предмет: Другие предметы,
автор: anonimka1892
Предмет: Алгебра,
автор: ketperyy67
Предмет: История,
автор: anaolgi275