1. Найти угол между плоскостью в с д и прямой аб (число и уравнение)
2. Уравнение высоты УФ и ее длину (число и уравнение)
3. определить фигуру, записать в каноническом виде (уравнение, слово
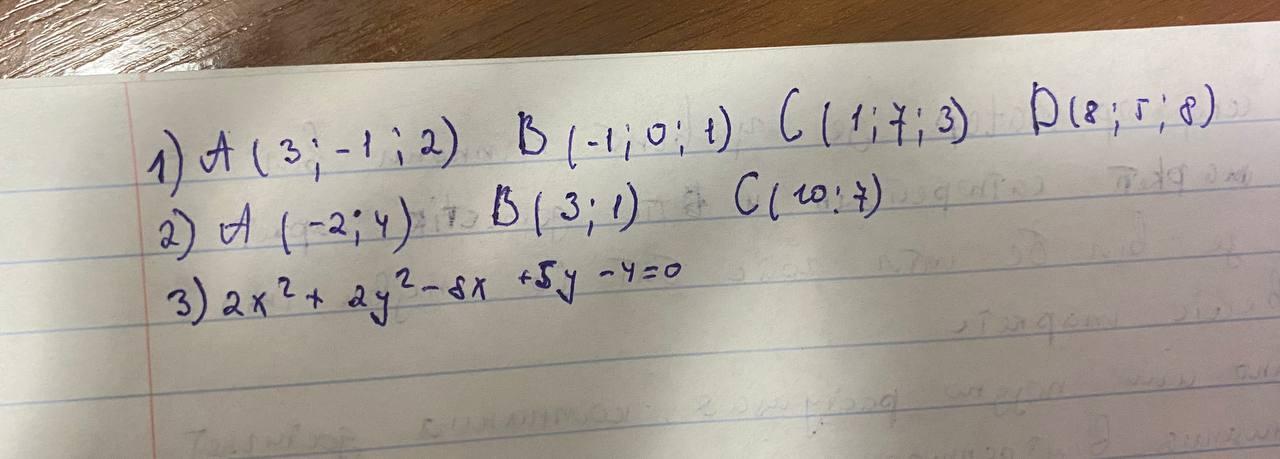
Ответы
1) Для составления уравнения плоскости используем формулу:
x - xB y - yB z - zB
xC - xB yC - yB zC - zB
xD - xB yD - yB zD – zB = 0
Подставим данные точек B, C, D и упростим выражение:
x - (-1) y – 0 z - 1
1 - (-1) 7 - 0 3 - 1
8 - (-1) 5 - 0 8 – 1 = 0
x - (-1) y - 0 z - 1
2 7 2
9 5 7 = 0.
(x - (-1))(7·7-2·5) - (y - )(2·7-2·9) + (z – 1)(2·5-7·9) = 0.
39(x - (-1)) + 4(y – 0) + (-53)(z – 1) = 0.
39x + 4y - 53z + 92 = 0.
Воспользуемся формулой канонического уравнения прямой:
x - xa = y – ya = z - za
xb – xa yb – ya zb - za
Подставим в формулу координаты точек А и В:
x - 3 = y - (-1) = z - 2
(-1) – 3 0 - (-1) 1 - 2
В итоге получено каноническое уравнение прямой:
x - 3 = y + 1 = z - 2
-4 1 -1
Найдем угол между прямой
(x – 3)/(-4) = (y + 1)/1 = (z – 2)/1
и плоскостью
39x + 4y - 53z + 92 = 0.
Направляющий вектор прямой имеет вид:
s = -4; 1; 1
Вектор нормали плоскости имеет вид:
q = 39; 4; -53
Вычислив угол между векторами, найдем угол между прямой и плоскостью:
sin φ = |cos ψ| = | s · q |/| s |·| q | =
= | sx · qx + sy · qy + sz · qz |/√(sx² + sy² + sz²) · √(qx² + qy² + qz²) =
= | 39 · (-4) + 4 · 1 + (-53) · 1 |/√(39² + 4² + (-53)²) ·√((-4)² + 1² + 1²) =
= | -156 + 4 - 53 |/√(1521 + 16 + 2809) · √(16 + 1 + 1) =
= 205/(√4346 · √18) = 205/√78228 =
= (5/318)·√2173 ≈ 0,7329473.
φ =arcsin 0,7329473 = 47,13405°.