Question

Перпендикуляр опущений із вершини прямокутника на діагональ ділить її у відношенні 1:3. Знайдіть довжину діагоналі якщо точка перетину діагоналей даного прямокутника віддалена від більшої його сторони на 3,6 дм.
ТРЕБА ДО 22:00 11.10.2023. ДОПОМОЖІТЬ ПРОШУ БУДЬ ЛАСКА
ДАЮ 40 БАЛІВ

Answer 1

Ответ:

14.4 дм

Объяснение:

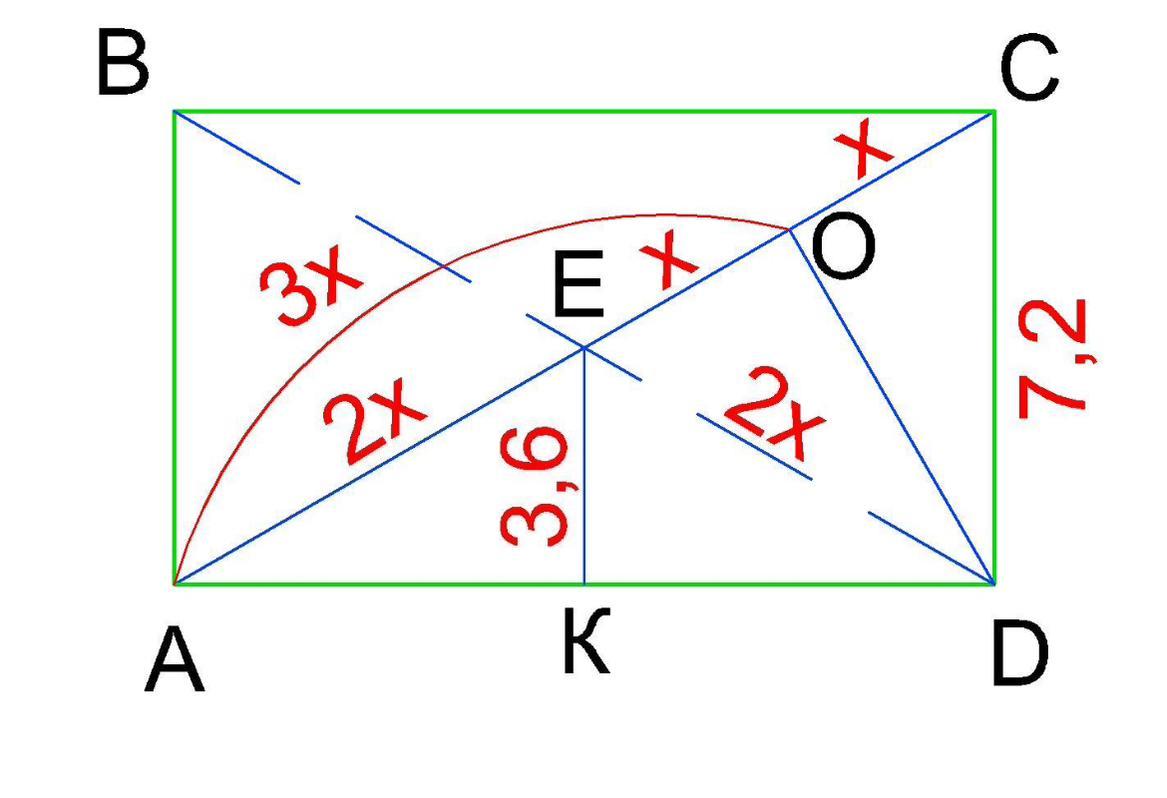
Побудуємо прямокутник ABCD, та проведемо в ньому діагоналі АС і BD, а також висоту DO до діагоналі АС і висоту EK із точки перетину діагоналей до більшої сторони AD.

Приймемо, що ОС=х,

тоді АС=4х.

Так як діагоналі прямокутника рівні і точкою перетину діляться навпіл, то АЕ=СЕ=ЕD=2х

і OE=CE-OC ⇒ OE=2x-x ⇒ OE=x.

Так як точка перетину діагоналей прямокутника є його геометричним центром, то CD=2EK=7.2 дм.

Тоді, із прямокутного ΔCDO маємо:

OD²=CD²-OC² ⇒ OD²=51.84 - x²

Із прямокутного ΔEDO маємо:

OD²=ED²-OE² ⇒ OD²=4x² - x² ⇒ OD²=3x²

Отримуємо вираз:

51.84 - x² = 3x²

4x²=51.84

x=3.6

Тоді довжина діагоналі:

АС=4х=14.4 дм

Answer 2

Побудуємо прямокутник ABCD, та проведемо в ньому діагоналі АС і BD, а також висоту DO до діагоналі АС і висоту EK із точки перетину діагоналей до більшої сторони AD.
Приймемо, що ОС=х,
тоді АС=4х.
Так як діагоналі прямокутника рівні і точкою перетину діляться навпіл, то АЕ=СЕ=ЕD=2х
і OE=CE-OC ⇒ OE=2x-x ⇒ OE=x.
Так як точка перетину діагоналей прямокутника є його геометричним центром, то CD=2EK=7.2 см.
Тоді, із прямокутного ΔCDO маємо:
OD²=CD²-OC² ⇒ OD²=51.84 - x²
Із прямокутного ΔEDO маємо:
OD²=ED²-OE² ⇒ OD²=4x² - x² ⇒ OD²=3x²
Отримуємо вираз:
51.84 - x² = 3x²
4x²=51.84
x=3.6
Тоді довжина діагоналі:
АС=4х=14.4 см