ТЕРМІНОВО 100 балів!!!!
Основою піраміди є прямокутник, діагональ якого дорівнює 12 см.
Площини двох бічних граней піраміди перпендикулярні до площини її основи, а дві інші грані утворюють із площиною основи кути 60° і 45°. Знайдіть площу бічної поверхні піраміди
Ответы
Ответ:
Площадь боковой поверхности пирамиды равна (18√6 + 54√3 + 54) см²
Объяснение:
Основой пирамиды является прямоугольник, диагональ которого равна 12 см.
Плоскости двух боковых граней пирамиды перпендикулярны плоскости ее основания, а две другие грани образуют с плоскостью основания углы 60° и 45°. Найдите площадь боковой поверхности пирамиды.
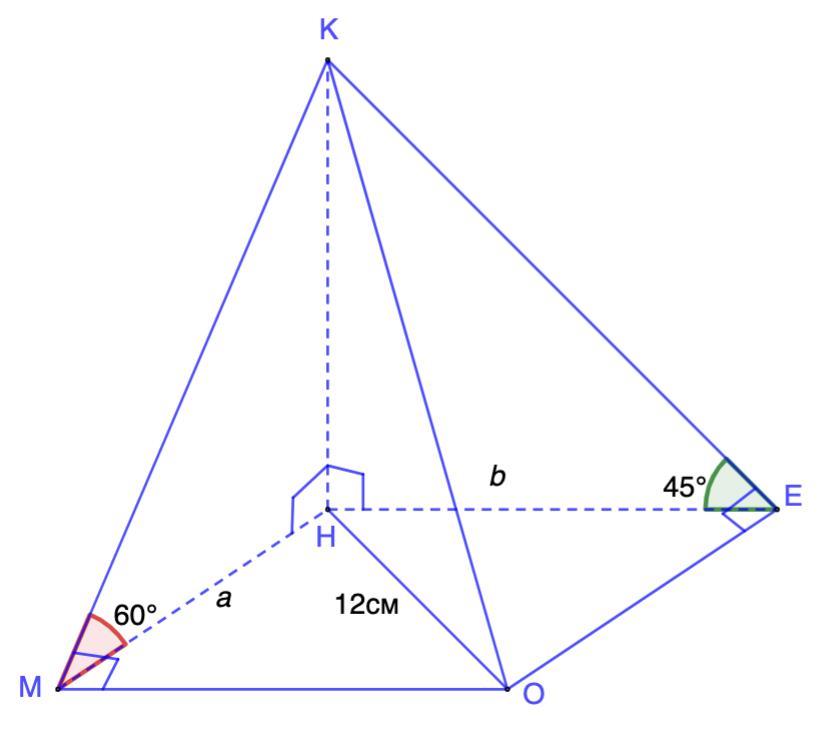
Дано: КМНЕО - пирамида;
МНЕО - прямоугольник;
НО = 12 см - диагональ;
ΔМКН ⊥ МНЕО; ΔНКЕ ⊥ МНЕО;
(МКО)^(МНЕО) = 60°; (ОКЕ)^(МНЕО) = 45°
Найти: Sбок.
Решение:
Определим углы между двумя наклонными гранями и основания.
- Угол между плоскостями — это угол между перпендикулярами, проведенными в данных плоскостях к линии пересечения плоскостей.
НМ ⊥ МО; НМ - проекция МК на МНЕО.
- Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.
⇒ МК ⊥ МО.
⇒ ∠ КМН = 60° - (МКО)^(МНЕО)
Аналогично:
∠КЕН = 45° - (ОКЕ)^(МНЕО)
Пусть стороны основания МН = ОЕ = а см, НЕ = МО = b см.
1. Рассмотрим ΔМКН - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠МКН = 90° - 60° = 30°
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒ МК = 2МН = 2а см.
По теореме Пифагора:
МК² = МН² + НК² ⇒ НК² = 4а² - а² = 3а² ⇒ НК = а√3 см.
2. Рассмотрим ΔНКЕ - прямоугольный.
∠НКЕ = 90° - 45° = 45°
- Если в треугольника два равных угла, то он равнобедренный.
⇒ НК = НЕ = b = а√3 см;
По теореме Пифагора:
КЕ² = НК² + НЕ² = 6а² ⇒ КЕ = а√6 см
3. Рассмотрим ΔМНО - прямоугольный;
По теореме Пифагора:
НО² = МН² + МО²
144 = а² + 3а² |:4
а² = 36
a = 6
⇒ а = 6 см; b = 6√3 см
4. Боковая поверхность данной пирамиды - четыре прямоугольных треугольника.
Поэтому Sбок. равна сумме площадей этих треугольников.
- Площадь прямоугольного треугольника равна половине произведения катетов.
1) ΔМКН.
МН = 6 см; НК = а√3 = 6√3 (см)
S(МКН) = 0,5 · 6 · 6√3 = 18√3 (см²)
2) ΔНКЕ.
НК = НЕ = 6√3 см;
S(НКЕ) = 0,5 · 6√3 · 6√3 = 54 (см²)
3) ΔМКО.
МК = 2а = 12 (см); МО = 6√3 см
S(МКО) = 0,5 · 12 · 6√3 = 36√3 (см²)
4) ΔОКЕ.
ОЕ = 6 см; КЕ = а√6 = 6√6 см.
S(ОКЕ) = 0,5 · 6 · 6√6 = 18√6 (см²)
Sбок. = 18√3 + 54 + 36√3 + 18√6 = (18√6 + 54√3 + 54) см²
#SPJ1