Предмет: Алгебра,
автор: sinelnikova0603
Алгебра, 8 клас!!!!!
Приложения:
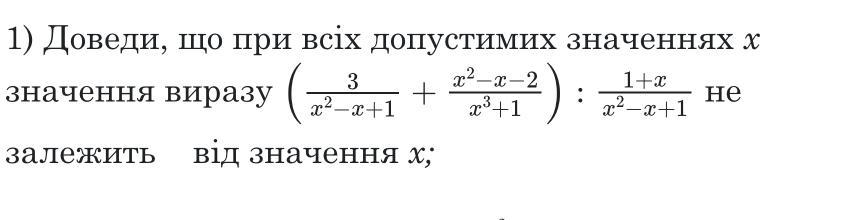
Ответы
Автор ответа:
0
После упрощения получили ответ , в котором не содержится переменная , значит значение выражения не зависит от этой переменной .
Похожие вопросы
Предмет: Қазақ тiлi,
автор: bstarts24
Предмет: Алгебра,
автор: anirggvga
Предмет: Английский язык,
автор: oleksandrabelikova7
Предмет: Алгебра,
автор: Аноним