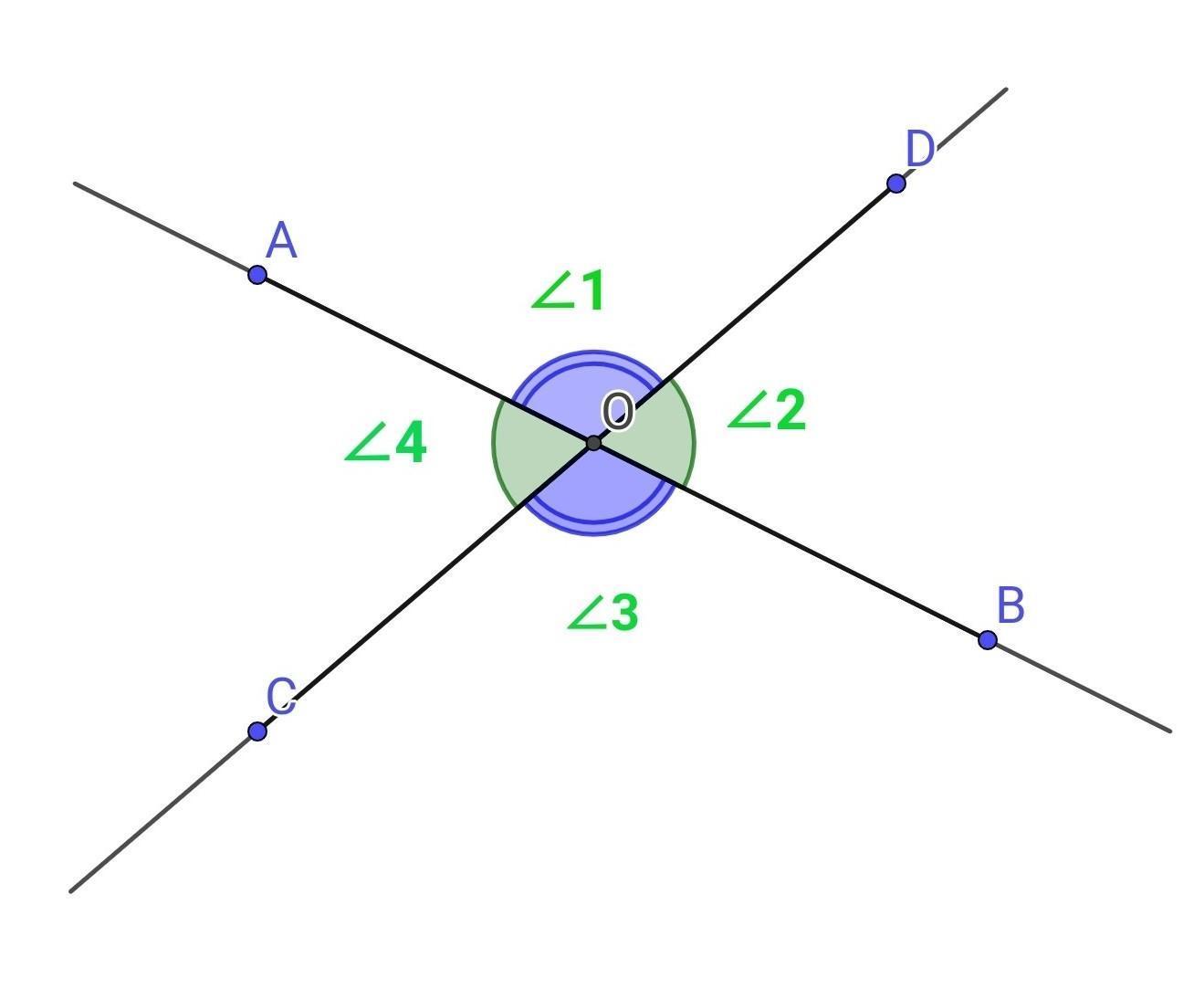
знайдіть величину кожного з кутів які утворилися при перетині двух прямих якщо:
1. сумма 2 з них = 96 градусів
2. різниця 2 з них = 62 градуси
3. усі кути рівні між собою
4. сумма трьох з них = 294 градуси
допожіть будь ласка, даю 100 балів!
Ответы
Ответ:
1) 48°, 48°, 132°, 132°.
2) 59°, 59°, 121°, 121°.
3) 90°, 90°, 90°, 90°.
4) 66°, 66°, 114°, 114°.
Объяснение:
Знайдіть величину кожного з кутів які утворилися при перетині двух прямих якщо:
1. сумма 2 з них = 96°
2. різниця 2 з них = 62°
3. усі кути рівні між собою
4. сумма трьох з них = 294°
При перетині двох прямих утворюються суміжні та вертикальні кути.
- Кути називаються вертикальними якщо вони утворені перетином двох прямих і не є прилеглими.
∠1 і ∠3, та ∠2 і ∠4 - вертикальні
- Вертикальні кути рівні.
∠1 = ∠3, та ∠2 = ∠4.
- Суміжні кути доповнюють один одного до 180°.
∠1 і ∠2, та ∠3 і ∠4 - суміжні кути. ∠1+∠2=180°, та ∠3+∠4=180°
Розв'язання
1.
Оскільки сума двох кутів не дорівнює 180°, то це вертикальні кути. Вони рівні. Величина яких дорівнює:
∠1 =∠3 = 96° : 2 = 48°,
∠2 є суміжним з ∠1. Тому:
∠1 +∠2=180°, ⇒ ∠2 = 180° - 48° = 132°
∠4 =∠2 = 132° - як вертикальні.
2.
При перетині двох прямих утворюються дві пари вертикальних кутів.
Нехай ∠2 = ∠4 = х - величина першої пари кутів,
∠1 = ∠3 = х + 62 - величина другої пари вертикальних кутів.
Два вертикальні кути різних пар утворюють суміжний кут, тому складаємо рівняння:
х + х + 62 = 180
2х = 180 - 62
2х = 118
х = 59
Отже, ∠2 = ∠4 = 59°, ∠1 = ∠3 = 59° + 62° = 121°
3.
Сума всіх кутів, що утворюються при перетині двох прямих, дорівнює 360°.
Отже, якщо вони рівні, то:
∠1 =∠2 =∠3 = ∠4 = 360° : 4 = 90°
4.
Величина четвертого кута, та відповідного вертикального для нього кута:
∠4 = ∠2 = 360° - 294° = 66°.
Тоді величина двох інших вертикальних кутів:
∠1 = ∠3 = 180° - 66° = 114°.
#SPJ1