Знайдіть допустимі значення змінної x²+x/4x²-4x+1
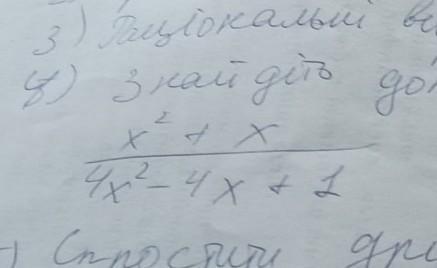
Ответы
Ответ:
Для нахождения допустимых значений переменной x в выражении (x² + x)/(4x² - 4x + 1), мы должны исследовать знаменатель и исключить значения x, при которых знаменатель обращается в ноль.
Знаменатель выражения равен 4x² - 4x + 1. Чтобы найти значения x, при которых знаменатель обращается в ноль, решим уравнение:
4x² - 4x + 1 = 0
Данное квадратное уравнение можно решить с помощью дискриминанта. Дискриминант D равен:
D = (-4)² - 4 * 4 * 1 = 16 - 16 = 0
Так как дискриминант равен нулю, уравнение имеет один корень. Решив уравнение, получим:
x = -(-4) / (2 * 4) = 4 / 8 = 1/2
Значит, при x = 1/2 знаменатель обращается в ноль.
Таким образом, допустимые значения переменной x для данного выражения - все значения x, кроме x = 1/2.
x²-x
________
4x²-4x+1
x²-x
x(x-1)=0
x1=0 x2=1
4x²-4x+1=0
D=b²-4•a•c=16-4•4•1=0
_______
x= -(-4)±√(-4)²-4•4+1/2•4
____
x=4±√16-16 /8
x=4±√0/8
x=4±0/8
x=4/8
сократим
x=1/2
вроде бы так, если не правильно прости пожалуйста.