Question

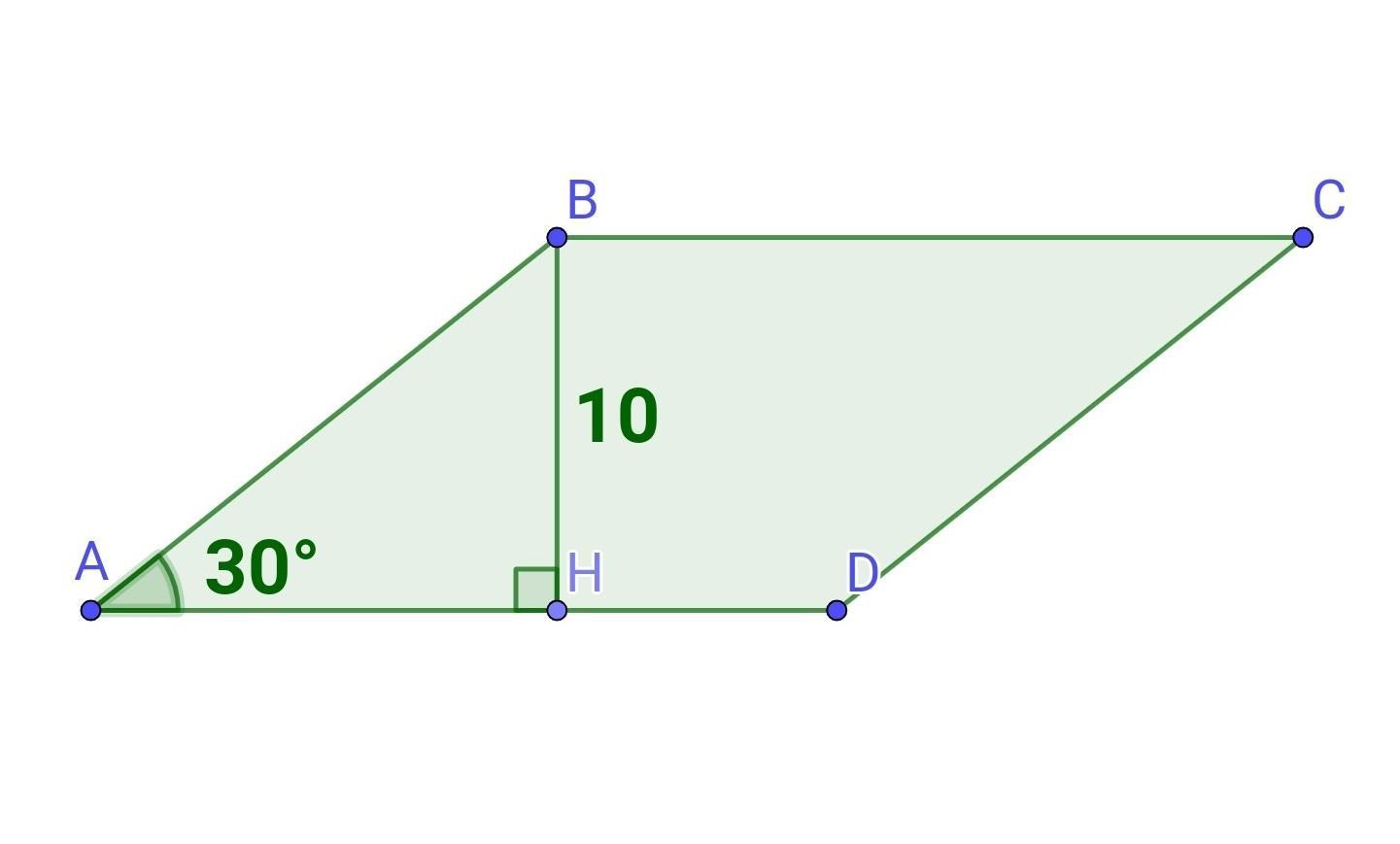
в паралелограмі abcd кут a дорівнює 30, BH перпендикуляр до сторони AD і дорівнює 10см знайдіть сторони паралелограма якщо його периметер дорівнює 147см (будь ласка с малюнком)

Answer 1

Ответ:

Сторони паралелограма дорівнюють 20 см і 53,5 см

Объяснение:

В паралелограмі ABCD кут A дорівнює 30, BH - перпендикуляр до сторони AD і дорівнює 10см. Знайдіть сторони паралелограма, якщо його периметер дорівнює 147см.

Нехай ABCD - даний паралелограм. ∠А=30°, BH - висота, BH=10 см, Р(ABCD)=147 см.

Знайдемо сторони AB, BC, CD, AD.

1. Розглянемо прямокутний трикутник АBH (∠H=90°).

∠A=30°, BH-катет, що лежить проти кута 30°.

ВН =½•АВ - за властивістю.

Тоді АВ = 2 • ВН = 2 • 10 = 20(см).

2. СD = АВ = 20 (см) - як протилежні сторони паралелограма.

3. Периметр паралелограма дорівнює подвоєної сумі його сусідніх сторін:

Р(ABCD) = 2•(AB+BC)

Тоді:

AB + BC = P(ABCD) : 2

AB + BC = 147 : 2 = 73,5(см)

ВС = 73,5 - 20 = 53,5(см)

4. AD = BC = 53,5 (см) - як протилежні сторони паралелограма.

Відповідь: AB=CD=20 см, AD=BC=53,5 см

#SPJ1